【题目】如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于![]() EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
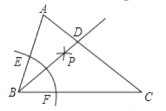
A.∠ADB=∠ABCB.AB=BDC.AC=AD+BDD.∠ABD=∠BCD
参考答案:
【答案】B
【解析】
根据作图方法可得BD平分∠ABC,进而可得∠ABD=∠DBC=![]() ∠ABC,然后根据条件∠ABC=2∠C可证明∠ABD=∠DBC=∠C,再根据三角形内角和外角的关系可得A说法正确;根据等角对等边可得DB=CD,进而可得AC=AD+BD,可得C说法正确;根据等量代换可得D正确.
∠ABC,然后根据条件∠ABC=2∠C可证明∠ABD=∠DBC=∠C,再根据三角形内角和外角的关系可得A说法正确;根据等角对等边可得DB=CD,进而可得AC=AD+BD,可得C说法正确;根据等量代换可得D正确.
由题意可得BD平分∠ABC,
A. ∵BD平分∠ABC,
∴∠ABD=∠DBC=![]() ∠ABC,
∠ABC,
∵∠ABC=2∠C,∠ADB=∠C+∠DBC,
∴∠ADB=2∠C,
∴∠ADB=∠ABC,故A不合题意;
B. ∵∠A≠∠ADB,
∴AB≠BD,故此选项符合题意;
C. ∵∠DBC=![]() ∠ABC,∠ABC=2∠C,
∠ABC,∠ABC=2∠C,
∴∠DBC=∠C,
∴DC=BD,
∵AC=AD+DC,
∴AC=AD+BD,故此选项不合题意;
D. ∵∠ABD=![]() ∠ABC,∠ABC=2∠C,
∠ABC,∠ABC=2∠C,
∴∠ABD=∠C,故此选项不合题意;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,将两个完全相同的三角形纸片 ABC 和 DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)如图2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落 在 AB 边上时,
①填空:线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,求证:S1=S2

(2)当△DEC 绕点 C 旋转到如图 3 所示的位置时,小明猜想(1) 中 S1 与 S2 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE 边上的高,请你证明小明的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为
 ,
, ,
, ,
, ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直角三角形ABC沿着斜边AC的方向平移到△DEF的位置(A、D. C. F四点在同一条直线上).直角边DE交BC于点G.如果BG=4,EF=12,△BEG的面积等于4,那么梯形ABGD的面积是( )

A.16B.20C.24D.28
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
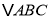 中,
中,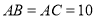 厘米,
厘米,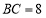 厘米,点
厘米,点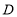 为
为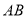 的中点.
的中点.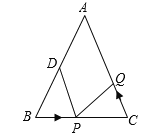
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,
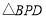 与
与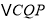 是否全等,请说明理由;
是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,
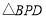 与
与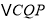 是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿
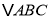 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在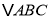 的哪条边上相遇?
的哪条边上相遇? -
科目: 来源: 题型:
查看答案和解析>>【题目】
 经过
经过 顶点
顶点 的一条直线,
的一条直线, .
. 分别是直线
分别是直线 上两点,且
上两点,且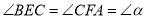 .
.(1)若直线
 经过
经过 的内部,且
的内部,且 在射线
在射线 上,请解决下面两个问题:
上,请解决下面两个问题:①如图1,若
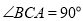 ,
, ,
,则
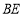
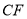 ;
;
 (填“
(填“ ”,“
”,“ ”或“
”或“ ”);
”);②如图2,若
 ,请添加一个关于
,请添加一个关于 与
与 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线
 经过
经过 的外部,
的外部, ,请提出
,请提出 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
相关试题

