【题目】如图,已知![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
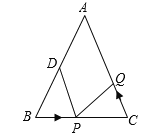
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等, ![]() 与
与![]() 是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿![]() 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
参考答案:
【答案】(1)①![]() ,理由见解析;②
,理由见解析;②![]() 秒,
秒,![]() 厘米/秒;(2)经过
厘米/秒;(2)经过![]() 秒,点
秒,点![]() 与点
与点![]() 第一次在边
第一次在边![]() 上相遇
上相遇
【解析】
(1)①根据“路程=速度×时间”可得![]() ,然后证出
,然后证出![]() ,根据等边对等角证出
,根据等边对等角证出![]() ,最后利用SAS即可证出结论;
,最后利用SAS即可证出结论;
②根据题意可得![]() ,若
,若![]() 与
与![]() 全等,则
全等,则![]() ,根据“路程÷速度=时间”计算出点P的运动时间,即为点Q运动的时间,然后即可求出点Q的速度;
,根据“路程÷速度=时间”计算出点P的运动时间,即为点Q运动的时间,然后即可求出点Q的速度;
(2)设经过![]() 秒后点
秒后点![]() 与点
与点![]() 第一次相遇,根据题意可得点
第一次相遇,根据题意可得点![]() 与点
与点![]() 第一次相遇时,点Q比点P多走AB+AC=20厘米,列出方程,即可求出相遇时间,从而求出点P运动的路程,从而判断出结论.
第一次相遇时,点Q比点P多走AB+AC=20厘米,列出方程,即可求出相遇时间,从而求出点P运动的路程,从而判断出结论.
解:(1)①∵![]() 秒,
秒,
∴![]() 厘米,
厘米,
∵![]() 厘米,点
厘米,点![]() 为
为![]() 的中点,
的中点,
∴![]() 厘米.
厘米.
又∵![]() 厘米,
厘米,
∴![]() 厘米,
厘米,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
在△BPD和△CQP中
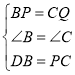
∴![]() .
.
②∵![]() ,
,
∴![]() ,
,
又∵![]() 与
与![]() 全等,
全等,
![]() ,
,
则![]() ,
,
∴点![]() ,点
,点![]() 运动的时间
运动的时间![]()
![]() 秒,
秒,
∴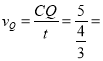
![]() 厘米/秒.
厘米/秒.
(2)设经过![]() 秒后点
秒后点![]() 与点
与点![]() 第一次相遇,
第一次相遇,
∵![]()
∴点![]() 与点
与点![]() 第一次相遇时,点Q比点P多走AB+AC=20厘米
第一次相遇时,点Q比点P多走AB+AC=20厘米
∴![]() ,
,
解得![]() 秒.
秒.
∴点![]() 共运动了
共运动了![]() 厘米.
厘米.
∵![]() ,
,
∴点![]() 、点
、点![]() 在
在![]() 边上相遇,
边上相遇,
∴经过![]() 秒,点
秒,点![]() 与点
与点![]() 第一次在边
第一次在边![]() 上相遇.
上相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于
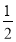 EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )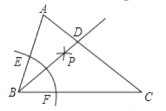
A.∠ADB=∠ABCB.AB=BDC.AC=AD+BDD.∠ABD=∠BCD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直角三角形ABC沿着斜边AC的方向平移到△DEF的位置(A、D. C. F四点在同一条直线上).直角边DE交BC于点G.如果BG=4,EF=12,△BEG的面积等于4,那么梯形ABGD的面积是( )

A.16B.20C.24D.28
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 经过
经过 顶点
顶点 的一条直线,
的一条直线, .
. 分别是直线
分别是直线 上两点,且
上两点,且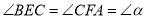 .
.(1)若直线
 经过
经过 的内部,且
的内部,且 在射线
在射线 上,请解决下面两个问题:
上,请解决下面两个问题:①如图1,若
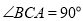 ,
, ,
,则
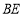
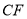 ;
;
 (填“
(填“ ”,“
”,“ ”或“
”或“ ”);
”);②如图2,若
 ,请添加一个关于
,请添加一个关于 与
与 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线
 经过
经过 的外部,
的外部, ,请提出
,请提出 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
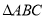 中,
中,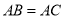 ,求证:
,求证: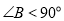 .下面给出运用反证法证明的四个步骤:①∴
.下面给出运用反证法证明的四个步骤:①∴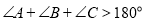 ,这与三角形内角和为
,这与三角形内角和为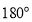 矛盾
矛盾②因此假设不成立.∴
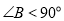
③假设在
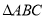 中,
中,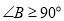
④由
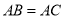 ,得
,得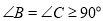 ,即
,即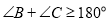
这四个步骤正确的顺序应是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线
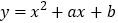 与
与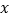 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线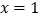 ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )A.
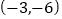 B.
B. 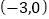 C.
C. 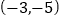 D.
D. 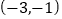
相关试题

