【题目】如图AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,
∠APB=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求PA及弦AB长.

参考答案:
【答案】(1)证明见解析;(2)PA=2![]() ,AB=2
,AB=2![]()
【解析】(1)证明:连接OB.
∵OA=OB,∴∠OBA=∠BAC=30°
∴∠AOB=180°-30°-30°=120°
∵PA切⊙O于点A,
∴OA⊥PA,即∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-120°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.
(2)解:连接OP.∵PA、PB是⊙O的切线,∴PA=PB,∠OPA=
∠OPB=![]() ∠APB=30°.
∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°
∴OP=2OA=2×2=4,
∴PA=![]() =
=![]() =2
=2![]()
∵PA=PB,∠APB=60°,∴PA=PB=AB=2![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(3yx2﹣2xy)﹣(4x2y﹣6xy﹣3),其中x=﹣1,y=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
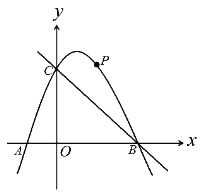
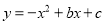 的图象与x轴交于A、B两点, 与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0))。点P是抛物线上一个动点,且在直线BC的上方.
的图象与x轴交于A、B两点, 与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0))。点P是抛物线上一个动点,且在直线BC的上方.(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形
 ,那么是否存在点P,使四边形
,那么是否存在点P,使四边形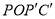 为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,使△BPC的面积最大,求出点P的坐标和△BPC的面积最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列关于x的函数中,一定是二次函数的是( )
A.y=x2B.y=ax2+bx+cC.y=8x D.y=x2(1+x)
-
科目: 来源: 题型:
查看答案和解析>>【题目】a的相反数的绝对值与3的和是正数,用不等式表示为 .
-
科目: 来源: 题型:
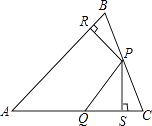
查看答案和解析>>【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的序号为( )
A.①②③
B.①②④
C.②③④
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
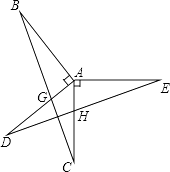
求证:
(1)△ABC≌△ADE;
(2)BC⊥DE.
相关试题

