【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的序号为( ) 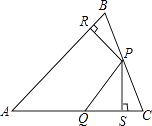
A.①②③
B.①②④
C.②③④
D.①②③④
参考答案:
【答案】D
【解析】解:∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2﹣PR2 , AS2=AP2﹣PS2 ,
∵AP=AP,PR=PS,
∴AR=AS,∴②正确;
∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP∥AR,∴③正确;
∵△ABC是等边三角形,
∴∠B=∠CAB=60°,AB=AC,
∵∠QAP=∠BAP,
∴BP=CP,
∵QP∥AB,
∴∠QPC=∠B=60°=∠C,
∴PQ=CQ,
∴△PQC是等边三角形,
∴PQ=CP=BP,∠SQP=60°=∠B,
∵PR⊥AB,PS⊥AC,
∴∠BRP=∠PSQ=90°,
在△BRP和△QSP中,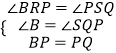 ,
,
∴△BRP≌△QSP,∴④正确;
连接RS,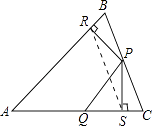
∵PR=PS,
∴点P在RS的垂直平分线上,
∵AS=AR,
∴点A在RS的垂直平分线上,
∴AP垂直平分RS,∴①正确.
所以答案是:D.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列关于x的函数中,一定是二次函数的是( )
A.y=x2B.y=ax2+bx+cC.y=8x D.y=x2(1+x)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,
∠APB=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求PA及弦AB长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】a的相反数的绝对值与3的和是正数,用不等式表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
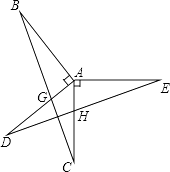
求证:
(1)△ABC≌△ADE;
(2)BC⊥DE. -
科目: 来源: 题型:
查看答案和解析>>【题目】材料:一般地,n个相同因数a相乘:记为an . 如23=8,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么(log216)2+
 log381= .
log381= . -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.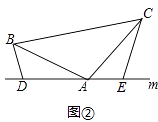
相关试题

