【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点P.
(1)以A点为位似中心,将△ABC在网格中放大成△AB1C1,使![]() =2,请画出△AB1C1;
=2,请画出△AB1C1;
(2)以P点为三角形的一个顶点,请画一个格点△PMN,使△PMN∽△ABC,且相似比为![]() .
.
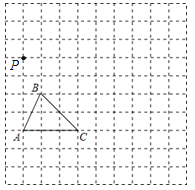
参考答案:
【答案】(1)答案见解析;(2)答案见解析.
【解析】【试题分析】(1)以A为位似中心,欲使![]() =2,即
=2,即![]() ,则△ABC与△AB1C1的相似比为
,则△ABC与△AB1C1的相似比为![]() ,即延长AB到B1 ,使AB=BB1,同样的方法,使AC=CC1,因为
,即延长AB到B1 ,使AB=BB1,同样的方法,使AC=CC1,因为![]() ,则△ABC
,则△ABC![]() △AB1C1,
△AB1C1,
(2)分别将个边长同时乘以![]() ,分别为
,分别为![]() ,利用勾股定理,分别找出来即可.
,利用勾股定理,分别找出来即可.
【试题解析】
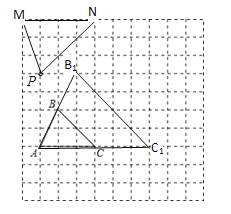
(1)如图,△AB1C1即为所求
(2)如图,△PMN即为所求(注意PM、PN、MN的长)。
-
科目: 来源: 题型:
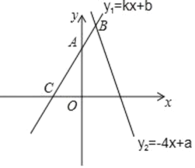
查看答案和解析>>【题目】一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)由图可知,不等式kx+b>0的解集是 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1.
①求点B的坐标;
②求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)
 +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果(2+
 )a-(1-
)a-(1- )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学;
(2)条形统计图中,m,n的值;
(3)扇形统计图中,求出艺术类读物所在扇形的圆心角的度数;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校应购买其他类读物多少册?
-
科目: 来源: 题型:
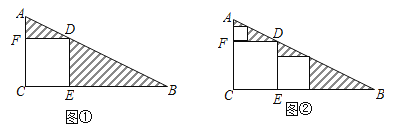
查看答案和解析>>【题目】三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图①的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积和为S1;按图②的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的两个三角形面积和为S2;继续操作下去…….
(1)如图①,求
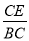 和S1的值;
和S1的值;(2)第n次剪取后,余下的所有三角形面积之和Sn为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的表达式;
(2)若直线AB上有一动点C,且
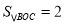 ,求点C的坐标.
,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案?
相关试题

