【题目】将平行四边形纸片![]() 按如图方式折叠,使点
按如图方式折叠,使点![]() 与
与![]() 重合,点
重合,点![]() 落到
落到![]() 处,折痕为
处,折痕为![]() .
.

(1)求证:![]() ;
;
(2)连结![]() ,判断四边形
,判断四边形![]() 是什么特殊四边形?证明你的结论.
是什么特殊四边形?证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)四边形AECF是菱形.证明见解析.
【解析】
试题分析:(1)根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′,AB=AD′,∠1=∠3,从而利用ASA判定△ABE≌△AD′F;
(2)四边形AECF是菱形,我们可以运用菱形的判定,有一组邻边相等的平行四边形是菱形来进行验证.
试题解析:(1)由折叠可知:∠D=∠D′,CD=AD′,
∠C=∠D′AE.
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,∠C=∠BAD.
∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,
即∠1+∠2=∠2+∠3.
∴∠1=∠3.
在△ABE和△AD′F中
∵
∴△ABE≌△AD′F(ASA).
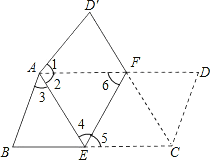
(2)四边形AECF是菱形.
证明:由折叠可知:AE=EC,∠4=∠5.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠5=∠6.
∴∠4=∠6.
∴AF=AE.
∵AE=EC,
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
又∵AF=AE,
∴平行四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD。
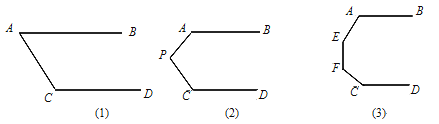
(1)在图(1)中,∠A+∠C= °.
(2)如图(2),试求∠A+∠P+∠C.
(3)如图(3),求∠A+∠E+∠F+∠C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发沿线段AB向终点B运动.作∠DEF=45°,与边BC相交于点F.

1)找出图中的一对相似三角形,并说明理由;
(2)当△BEF为等腰三角形时,求AE的长;
(3)求动点E从点A出发沿线段AB向终点B运动的过程中点F的运动路线长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片
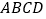 沿对角线
沿对角线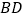 折叠,点
折叠,点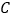 落在点
落在点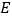 处,
处,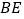 交
交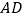 于点
于点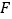 ,连结
,连结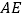 .证明:(1)BF=DF.(2)若BC=8,DC=6,求BF的长。
.证明:(1)BF=DF.(2)若BC=8,DC=6,求BF的长。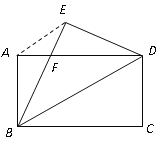
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各线段的长度成比例的是( )
A. 2 cm,5 cm,6 cm,8 cm B. 1 cm,2 cm,3 cm,4 cm
C. 3 cm,6 cm,7 cm,9 cm D. 3 cm,6 cm,9 cm,18 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组图形中,一定相似的是( )
A. 正方形与矩形 B. 正方形与菱形
C. 菱形与菱形 D. 正五边形与正五边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a是偶数时,(x﹣y)a(y﹣x)b与(y﹣x)a+b的关系是( )
A.相等
B.互为倒数
C.互为相反数
D.无法确定
相关试题

