【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是(把你认为正确结论的序号都填上.) 
参考答案:
【答案】①③④
【解析】解:∵△ABC为等边三角形,
∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,
∴∠BAE=∠ABC,
∴AE∥BC,所以①正确;
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,所以③正确;
∴∠BDE=60°,
∵∠BDC=∠BAC+∠ABD>60°,
∴∠ADE≠∠BDC,所以②错误;
∵△BDE是等边三角形,
∴DE=BD=4,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+4=5+4=9,所以④正确.
故答案为①③④.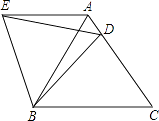
先根据等边三角形的性质得BA=BC,∠ABC=∠C=∠BAC=60°,再根据旋转的性质得到∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,所以∠BAE=∠ABC=60°,则根据平行线的判定方法即可得到AE∥BC;由△BCD绕点B逆时针旋转60°,得到△BAE得到BD=BE,∠DBE=60°,则可判断△BDE是等边三角形;根据等边三角形的性质得∠BDE=60°,而∠BDC>60°,则可判断∠ADE≠∠BDC;由△BDE是等边三角形得到DE=BD=4,再利用△BCD绕点B逆时针旋转60°,得到△BAE,则AE=CD,所以△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y=
 (k2>0)在第一象限的图象交于C,D两点,点O为坐标原点,△AOB的面积为
(k2>0)在第一象限的图象交于C,D两点,点O为坐标原点,△AOB的面积为 ,点C的横坐标为1.
,点C的横坐标为1.(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某天早上,一辆交通巡逻车从A地出发,在东西向的马路上巡视,中午到达B地,如果规定向东行驶为正,向西行驶为负,行驶纪录如下:(单位:km)
第一次
第二次
第三次
第四次
第五次
第六次
第七次
+15
-8
+6
+12
-4
+5
-10
(1)B地在A地哪个方向,与A地相距多少千米?
(2)巡逻车在巡逻过程中,离开A地最远是多少千米?
(3)若每km耗油0.1升,问共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形。



(1)拼成的正方形的面积与边长分别是多少?
(2)请在3×3方格图中,找出连接四个格点组成面积为5的正方形,并在图中画出虚线。
(3)你能把十个小正方形组成的图形纸,剪两刀并拼成正方形吗?若能,则它的边长是多少?并在图中画出裁剪的线。


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数
 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=
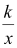 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).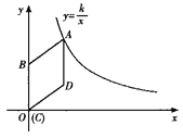
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
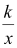 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
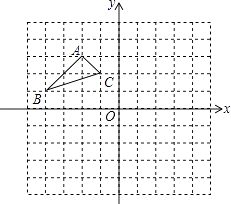
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1 , (只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2 , (只画出图形),写出B2和C2的坐标.
相关试题

