【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
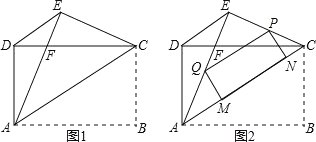
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
参考答案:
【答案】(1)证明见解析;(2)DF=![]() .(3) PE=
.(3) PE=![]() 时,矩形PQMN的面积最大,最大面积为3.
时,矩形PQMN的面积最大,最大面积为3.
【解析】试题分析:(1)由矩形和翻折的性质可知AD=CE,DC=EA,根据“SSS”可求得△DEC≌△EDA;
(2)根据勾股定理即可求得.
(3)由矩形PQMN的性质得PQ∥CA,所以![]() ,从而求得PQ,由PN∥EG,得出
,从而求得PQ,由PN∥EG,得出![]() ,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
试题解析:(1)由矩形和翻折的性质可知:AD=CE,DC=EA,
在△ADE与△CED中,
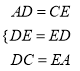
∴△DEC≌△EDA(SSS);
(2)如图1,
∵∠ACD=∠BAC,∠BAC=∠CAE,
∴∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4-x,
在Rt△ADF中,AD2+DF2=AF2,
即32+x2=(4-x)2,
解得:x=![]() ,
,
即DF=![]() .
.
(3)如图2,
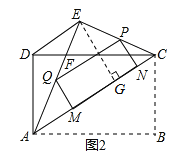
由矩形PQMN的性质得PQ∥CA
∴![]()
又∵CE=3,AC=![]() =5
=5
设PE=x(0<x<3),则![]() ,即PQ=
,即PQ=![]() x
x
过E作EG⊥AC于G,则PN∥EG,
∴![]()
又∵在Rt△AEC中,EGAC=AECE,解得EG=![]() ,
,
∴![]() =
=![]() ,即PN=
,即PN=![]() (3-x),
(3-x),
设矩形PQMN的面积为S,
则S=PQPN=-![]() x2+4x=-
x2+4x=-![]() (x-
(x-![]() )2+3(0<x<3)
)2+3(0<x<3)
所以当x=![]() ,即PE=
,即PE=![]() 时,矩形PQMN的面积最大,最大面积为3.
时,矩形PQMN的面积最大,最大面积为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14 m的D处有一大坝,背水坡CD的坡度i=1∶2,坝高CF为2 m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2 m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域,
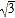 ≈1.732,
≈1.732, ≈1.414)
≈1.414)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=
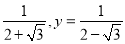 ;
;(1)求x2+y2﹣xy的值;
(2)若x的小数部分为a,y的小数部分为b,求(a+b)2+
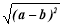 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织植树活动,按年级将七、八、九年级学生分成三个植树队,七年级植树x棵,八年级种的数比七年级种的数的2倍少26棵,九年级种的树比八年级种的树的一半多42棵.
(1)请用含x的式子表示三个队共种树多少棵.
(2)若这三个队共种树423棵,请你求出这三队各种了多少棵树.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
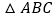 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点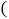 点D不与B,C重合
点D不与B,C重合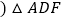 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.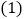 如图1,求证:
如图1,求证: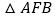 ≌
≌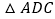 ;
; 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由; 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
-
科目: 来源: 题型:
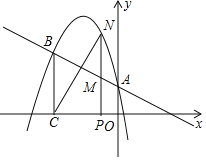
查看答案和解析>>【题目】如图所示,二次函数y=ax2﹣
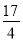 x+c的图象经过点A(0,1),B(﹣3,
x+c的图象经过点A(0,1),B(﹣3, 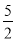 ),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
),A点在y轴上,过点B作BC⊥x轴,垂足为点C.(1)求直线AB的解析式和二次函数的解析式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)点N是二次函数图象上一点(点N在AB上方),是否存在点N,使得BM与NC相互垂直平分?若存在,求出所有满足条件的N点的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为( ,﹣2);⑤当x<
,﹣2);⑤当x< 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )
A. 3个 B. 4个 C. 5个 D. 6个
相关试题

