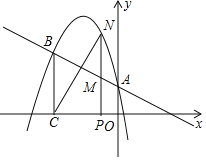
【题目】如图所示,二次函数y=ax2﹣![]() x+c的图象经过点A(0,1),B(﹣3,
x+c的图象经过点A(0,1),B(﹣3, ![]() ),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
(1)求直线AB的解析式和二次函数的解析式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)点N是二次函数图象上一点(点N在AB上方),是否存在点N,使得BM与NC相互垂直平分?若存在,求出所有满足条件的N点的坐标;若不存在,说明理由.
参考答案:
【答案】(1)y=﹣![]() x+1;y=﹣
x+1;y=﹣![]() x2﹣
x2﹣![]() x+1;(2)当m=﹣
x+1;(2)当m=﹣![]() 时,MN取最大值,最大值为
时,MN取最大值,最大值为![]() ;(3)存在点N,使得BM与NC相互垂直平分,点N的坐标为(﹣1,4)
;(3)存在点N,使得BM与NC相互垂直平分,点N的坐标为(﹣1,4)
【解析】试题分析:(1)根据已知点的坐标利用待定系数法即可得出结论;
(2)设点N的坐标为![]() 则点M的坐标为
则点M的坐标为
![]() 用含
用含![]() 的代数式表示出来
的代数式表示出来![]() ,结合二次函数的性质即可解决最值问题;
,结合二次函数的性质即可解决最值问题;
(3)假设存在,设点N的坐标为![]() 连接
连接![]() ,当四边形
,当四边形![]() 为菱形时,
为菱形时, ![]() 与
与![]() 相互垂直平分,根据
相互垂直平分,根据![]() 算出
算出![]() 的值,从而得出点
的值,从而得出点![]() 的坐标,再去验证
的坐标,再去验证![]() 是否等于
是否等于![]() ,由此即可得出结论.
,由此即可得出结论.
试题解析:(1)设直线AB的解析式为:y=kx+b,
∴
∴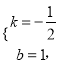
∴直线AB的解析式为: ![]()
把![]() 代入
代入![]() 得,
得, 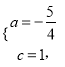
∴二次函数的解析式为: ![]()
(2)设点N的坐标为![]() 则点M的坐标为
则点M的坐标为
![]()
![]()
∴当![]() 时,MN取最大值,最大值为
时,MN取最大值,最大值为![]()
(3)假设存在,设点N的坐标为![]() 连接BN、CM,如图所示.
连接BN、CM,如图所示.
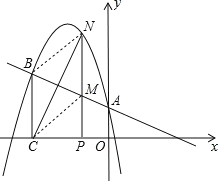
若要BM与NC相互垂直平分,只需四边形BCMN为菱形即可。
∵点B坐标为![]() 点C的坐标为(3,0),
点C的坐标为(3,0),
∴BC=52.
∵四边形BCMN为菱形,
![]() 解得:
解得: ![]()
当m=2时,点N的坐标为![]()
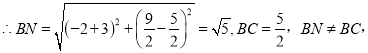
故m=2(舍去);
当m=1时,点N的坐标为(1,4),
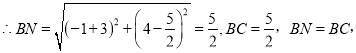
∴点N(1,4)符合题意.
故存在点N,使得BM与NC相互垂直平分,点N的坐标为(1,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织植树活动,按年级将七、八、九年级学生分成三个植树队,七年级植树x棵,八年级种的数比七年级种的数的2倍少26棵,九年级种的树比八年级种的树的一半多42棵.
(1)请用含x的式子表示三个队共种树多少棵.
(2)若这三个队共种树423棵,请你求出这三队各种了多少棵树.
-
科目: 来源: 题型:
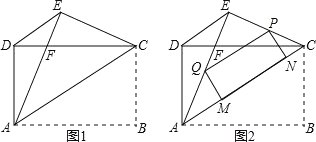
查看答案和解析>>【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点 点D不与B,C重合
点D不与B,C重合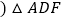 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF. 如图1,求证:
如图1,求证: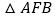 ≌
≌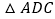 ;
;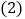 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;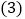 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问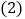 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为( ,﹣2);⑤当x<
,﹣2);⑤当x< 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )
A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,当△ABC为正三角形时,点E是否AC的中点?为什么?

相关试题

