【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
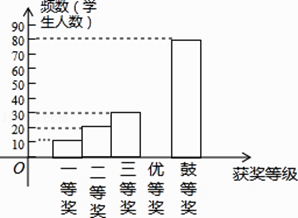
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
参考答案:
【答案】
(1)60;0.15;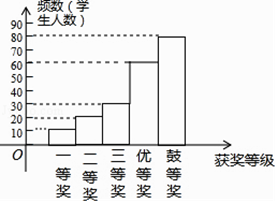
(2)解:优胜奖所在扇形的圆心角为0.30×360°=108°
(3)解:列表:甲乙丙丁分别用ABCD表示,
A | B | C | D | |
A | AB | AC | AD | |
B | BA | BC | BD | |
C | CA | CB | CD | |
D | DA | DB | DC |
∵共有12种等可能的结果,恰好选中A、B的有2种,
画树状图如下:
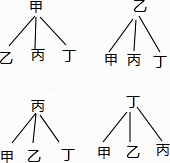
∴P(选中A、B)= ![]() =
= ![]()
【解析】解:(1)样本总数为10÷0.05=200人, a=200﹣10﹣20﹣30﹣80=60人,
b=30÷200=0.15,
故答案为60,0.15;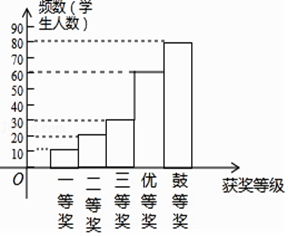
(1)根据公式频率=频数÷样本总数,求得样本总数,再根据公式得出a,b的值即可;(2)根据公式优胜奖对应的扇形圆心角的度数=优胜奖的频率×360°计算即可;(3)画树状图或列表将所有等可能的结果列举出来,利用概率公式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知凸四边形ABCD中,∠A=∠C=90°.


(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点
 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米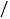 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米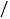 秒,则当△BPD与△CQP全等时,v的值为( )
秒,则当△BPD与△CQP全等时,v的值为( )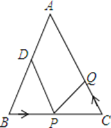
A. 2.5 B. 3 C. 2.25或3 D. 1或5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= .
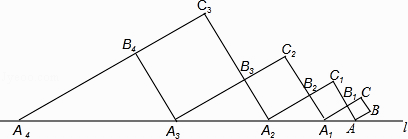
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列两材料,并解决相关的问题.
(材料一)按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为
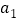 ,依此类推,排在第
,依此类推,排在第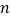 位的数称为第
位的数称为第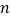 项,记为
项,记为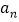 .一般地,若果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫作等比数列,这个常数叫作等比数列的公比,公比通常用字母
.一般地,若果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫作等比数列,这个常数叫作等比数列的公比,公比通常用字母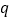 表示
表示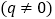 ,如数列
,如数列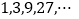 为等比数列,其中
为等比数列,其中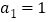 ,公比
,公比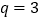 .
.(材料二)为了求
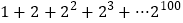 的值.可令
的值.可令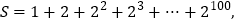
则
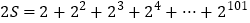 , 因此
, 因此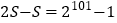 ,所以
,所以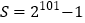 ,
,即
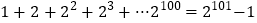
(1)等比数列
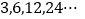 的公比
的公比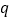 为_________,第6项是________
为_________,第6项是________(2)如果一个数列
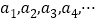 是等比数列,且公比为
是等比数列,且公比为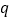 ,那么根据定义可得到
,那么根据定义可得到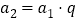 ,
,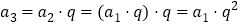 ,
,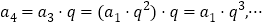 ,由此可得
,由此可得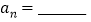 (用
(用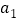 和
和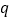 的代数式表示)
的代数式表示)(3)若某等比数列的公比
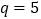 ,第2项
,第2项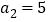 ,则它的第1项
,则它的第1项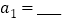 ,第4项
,第4项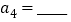 ,并求出
,并求出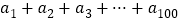 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点A,O,B表示的数分别为-3,0,1,点P为数轴上任意一点,其表示的数为x.
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)若点P到点A,点B的距离之和最小,则整数x是____________ ;
(3)当点P到点A,点B的距离之和是6时,求x的值;
(4)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动多少秒时,点P到点E,点F的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=
 (m≠0)交于点A(2,﹣3)和点B(n,2).
(m≠0)交于点A(2,﹣3)和点B(n,2). 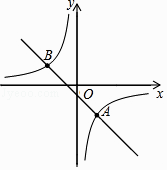
(1)求直线与双曲线的表达式;
(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
(m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
相关试题

