【题目】某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,5个福娃2枚徽章145元,10个福娃3枚徽章280元(5个福娃为1套),则:
(1)一套“福娃”玩具和一枚徽章的价格各是多少元?
(2)买5套“福娃”玩具和10枚徽章共需要多少元?
参考答案:
【答案】(1)一套“福娃”玩具的价格为125元,一枚徽章的价格为10元;(2)买5套“福娃”玩具和10枚徽章共需要725元.
【解析】
(1)设一套“福娃”玩具的价格为x元,一枚徽章的价格为y元,根据“5个福娃2个徽章145元,10个福娃3个徽章280元(5个福娃为1套)”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据总价=单价×数量,即可求出结论.
(1)设一套“福娃”玩具的价格为x元,一枚徽章的价格为y元,
依题意,得:![]() ,
,
解得:![]() .
.
答:一套“福娃”玩具的价格为125元,一枚徽章的价格为10元.
(2)125×5+10×10=725(元).
答:买5套“福娃”玩具和10枚徽章共需要725元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 (2)
(2)
(3)
 (4)
(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
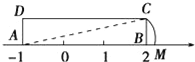
【答案】
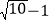
【解析】AC=AM=
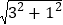 =
=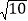 ,∴AM=
,∴AM=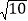
【题型】填空题
【结束】
11【题目】在△ABC中,AB=10,AC=2
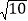 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:
①ac<0; ②当x>1时,y的值随x值的增大而减小;
③当 时,
时,  ; ④3是方程ax2+(b﹣1)x+c=0的一个根.
; ④3是方程ax2+(b﹣1)x+c=0的一个根.
其中正确的结论是(填正确结论的序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个项点的坐标分别为A (3. 3),B (-3, 0), C (0. -2).
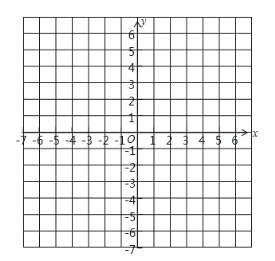
(1)在下面的平面直角坐标系中分别描出A,B, C三点,并画出△ABC;
(2)将(1)中的△ABC向上平移3个单位长度,向左中移2个单位长度,得到△
 在图中画出△
在图中画出△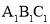 ,请分别写出A1、B1、C1三点的坐标.
,请分别写出A1、B1、C1三点的坐标.(3)求△ABC的面积.
相关试题

