【题目】已知:如图1,四边形ABCD是平行四边形,E,F是对角线AC上的两点,AE=CF.
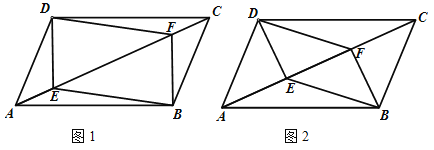
(1)求证:四边形DEBF是平行四边形;
(2)如果AE=EF=FC,请直接写出图中2所有面积等于四边形DEBF的面积的三角形.
参考答案:
【答案】(1)见解析;(2)△ADF,△CDE,△CBE,△ABF.
【解析】
(1)由四边形ABCD是平行四边形得出OA=OC,OB=OD,因为AE=CF可推出OE=OF,由对角线互相平分的四边形是平行四边形,可证结论;
(2)AE=EF=FC可知![]() ,故而可推面积等于四边形DEBF的面积的三角形有:△ADF,△CDE,△CBE,△ABF.
,故而可推面积等于四边形DEBF的面积的三角形有:△ADF,△CDE,△CBE,△ABF.
(1)证明:
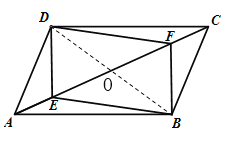
连接BD交AC于点O,
∵平行四边形ABCD
∴OA=OC,OB=OD
∵AE=CF
∴OE=OF
∴四边形DEBF为平行四边形;
(2)由AE=EF=FC可知![]()
故面积等于四边形DEBF的面积的三角形有:△ADF,△CDE,△CBE,△ABF;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.

(1)写出商场销售这种工具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布
次数
60≤x<80
80≤x<100
100≤x<120
频数
1
2
25
次数
120≤x<140
140≤x<160
160≤x<180
频数
15
5
2
(1)全班有多少学生?
(2)组距是多少?组数是多少
(3)跳绳次数x在100≤x<140范围的学生占全班学生的百分之几?
(4)画出适当的统计图表示上面的信息.
(5)你怎样评价这个班的跳绳成绩?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,海中有一个小岛
 ,它的周围14海里内有暗礁,在小岛正西方有一点
,它的周围14海里内有暗礁,在小岛正西方有一点 测得在北偏东60°方向上有一灯塔
测得在北偏东60°方向上有一灯塔 ,灯塔
,灯塔 在小岛
在小岛 北偏东15°方向上20海里处,渔船跟踪鱼群沿
北偏东15°方向上20海里处,渔船跟踪鱼群沿 方向航行,每小时航行
方向航行,每小时航行 海里.
海里.(1)如果渔船不改变航向继续航行,有没有触礁危险?请说明理由.
(2)求渔船从
 点处航行到灯塔
点处航行到灯塔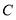 ,需要多少小时?
,需要多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】圣母大学计算机系的史戈宇教授带一家人去旅行,途中汽车被劫走报警911,警察无作为,汽车上安装的MS系统,可以提示汽车与手机APP间的直线距离。史教授用“贪心算法”把被盗车辆位置确定在了图中灰色的区域里,这是一个以暴乱和枪击闻名的地区。当史教授开车从E向A的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从A向F的方向行驶时,汽车与手机APP问的直线距离逐渐变大.当史教授开车从F向B的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从B向G的方向行驶时,汽车与手机APP间的直线距离逐渐变大. 史教授再次报警后,警察根据史教授确定的被盗汽车的位置,很快找到了被盗汽车根据你学的数学知识,在图中,画出被盗汽车的位置.

-
科目: 来源: 题型:
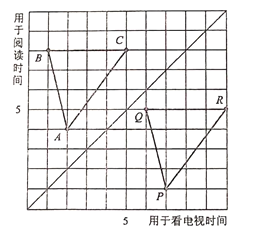
查看答案和解析>>【题目】图中,点A,B,C,P,Q,R显示了6名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h)
(1)用有序数对表示图中点A,B,C,P,Q,R
(2)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(3)三角形ABC的图形经过怎样的变换后得到三角形PQR的图形?其中点A对应点P,点B对应点Q,点C对应点R
-
科目: 来源: 题型:
查看答案和解析>>【题目】张翔上午7:30出发,从学校骑自行车去县城,路程全长20km,中途因道路施工步行一段路.他步行的平均速度是5km/h
(1)若张翔骑车的平均速度是15km/h,当天上午9:00到达县城,则他骑车与步行各用多少时间?
(2)若张翔必须在当天上午9:00之前赶到县城,他的步行平均速度不变,则他骑车的平均速度应在什么范围内?
相关试题

