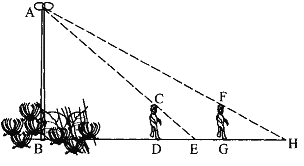
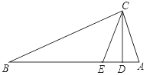
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
参考答案:
【答案】路灯杆AB的高度为6.0m.
【解析】试题分析:根据AB⊥BH,CD⊥BH,FG⊥BH,可得:△ABE∽△CDE,则有![]() 和
和![]() ,从而得到
,从而得到![]() ,从而求出BD的长,再代入前面任意一个等式中,即可求出AB.
,从而求出BD的长,再代入前面任意一个等式中,即可求出AB.
试题解析:解:根据题意得:AB⊥BH,CD⊥BH,FG⊥BH.
在Rt△ABE和Rt△CDE中,∵AB⊥BH,CD⊥BH,∴CD∥AB,可证得:
△ABE∽△CDE,∴![]() ①,同理:
①,同理:![]() ②,又CD=FG=1.7m,由①、②可得:
②,又CD=FG=1.7m,由①、②可得:![]() ,即
,即![]() ,解之得:BD=7.5m,将BD=7.5代入①得:AB=5.95m≈6.0m.
,解之得:BD=7.5m,将BD=7.5代入①得:AB=5.95m≈6.0m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1).若以C,D,E(E在格点上)为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
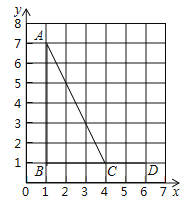
A. (6,0) B. (4,2) C. (6,5) D. (6,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在暗室做小孔成像实验.如图1,固定光源(线段MN)发出的光经过小孔(动点K)成像(线段M'N')于足够长的固定挡板(直线l)上,其中MN// l.已知点K匀速运动,其运动路径由AB,BC,CD,DA,AC,BD组成.记它的运动时间为x,M'N'的长度为y,若y关于x的函数图象大致如图2所示,则点K的运动路径可能为( )
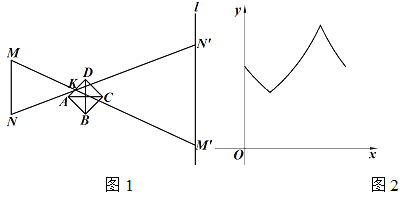
A. A→B→C→D→A B. B→C→D→A→B
C. B→C→A→D→B D. D→A→B→C→D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于依次排列的多项式x+a,x+b,x+c,x+d(a,b,c,d是常数),当它们满足在
 ,且M为常数时,则称a,b,c,d是一组平衡数,M是该组平衡数的平衡因子,例如:对于多项式x+2,x+1,x+6,x+5,因为
,且M为常数时,则称a,b,c,d是一组平衡数,M是该组平衡数的平衡因子,例如:对于多项式x+2,x+1,x+6,x+5,因为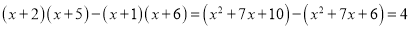 ,所以2,1,6,5是一组平衡数,4是该组平衡数的平衡因子.
,所以2,1,6,5是一组平衡数,4是该组平衡数的平衡因子.(1)已知2,4,7,9是一组平衡数,求该组平衡数的平衡因子M;
(2)若a,b,c,d是一组平衡数,a=-4,d=3,请直接写出组b,c的值;
(3)当a,b,c,d之间满是什么数量关系时,它们是一组平衡数,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
相关试题

