【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.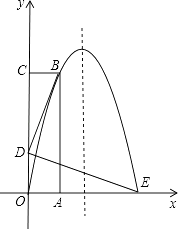
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标.
参考答案:
【答案】
(1)
解:将点B(1,4),E(3,0)的坐标代入抛物线的解析式得: ![]() ,
,
解得: ![]() ,
,
抛物线的解析式为y=﹣2x2+6x
(2)
解:如图1所示;
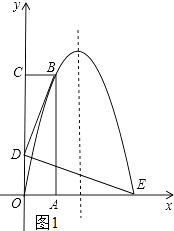
∵BD⊥DE,
∴∠BDE=90°.
∴∠BDC+∠EDO=90°.
又∵∠ODE+∠DEO=90°,
∴∠BDC=∠DE0.
在△BDC和△DOE中, 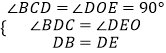 ,
,
∴△BDC≌△DEO(AAS).
∴OD=AO=1.
∴D(0,1)
(3)
解:如图2所示:作点B关于抛物线的对称轴的对称点B′,连接B′D交抛物线的对称轴与点M.

∵x=﹣ ![]() =
= ![]() ,
,
∴点B′的坐标为(2,4).
∵点B与点B′关于x= ![]() 对称,
对称,
∴MB=B′M.
∴DM+MB=DM+MB′.
∴当点D、M、B′在一条直线上时,MD+MB有最小值(即△BMD的周长有最小值).
∵由两点间的距离公式可知:BD= ![]() =
= ![]() ,DB′=
,DB′= ![]() =
= ![]() ,
,
∴△BDM的最小值= ![]() +
+ ![]() .
.
设直线B′D的解析式为y=kx+b.
将点D、B′的坐标代入得: ![]() ,
,
解得: ![]() ,
,
∴直线DB′的解析式为y= ![]() x+1.
x+1.
将x= ![]() 代入得:y=
代入得:y= ![]() .
.
∴M( ![]() ,
, ![]() )
)
【解析】(1)将点B(1,4),E(3,0)的坐标代入抛物线的解析式,得到关于a、b的方程组,求得a、b的值,从而可得到抛物线的解析式;(2)依据同角的余角相等证明∠BDC=∠DE0,然后再依据AAS证明△BDC≌△DEO,从而得到OD=AO=1,于是可求得点D的坐标;(3)作点B关于抛物线的对称轴的对称点B′,连接B′D交抛物线的对称轴与点M.先求得抛物线的对称轴方程,从而得到点B′的坐标,由轴对称的性质可知当点D、M、B′在一条直线上时,△BMD的周长有最小值,依据两点间的距离公式求得BD和B′D的长度,从而得到三角形的周长最小值,然后依据待定系数法求得D、B′的解析式,然后将点M的横坐标代入可求得点M的纵坐标.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)

(1)到终点下车还有________人.
(2)车行驶在那两站之间车上的乘客最多?________站和________站
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是中国古代著名的“杨辉三角形”的示意图.图中填入的所有数的总和等于()

A. 126 B. 127 C. 128 D. 129
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P.
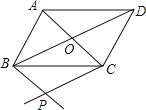
(1)判断四边形BPCO的形状,并说明理由;
(2)若将平行四边形ABCD改为菱形ABCD,其他条件不变,得到的四边形BPCO是什么四边形,并说明理由;
(3)若得到的是正方形BPCO,则四边形ABCD是 .(选填平行四边形、矩形、菱形、正方形中你认为正确的一个)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将连续正整数按如下规律排列:
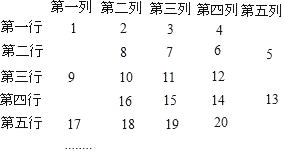
若正整数567位于第a行,第b列,则a与b的和是( )
A. 256 B. 239 C. 159 D. 145
-
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2015=( )
A. (31,50) B. (32,47) C. (33,46) D. (34,42)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将自然数按以下规律排列:

表中数2在第二行第一列,与有序数对(2,1)对应,数5与(1,3)对应,数14与(3,4)对应,根据这一规律,数2014对应的有序数对为_____.
相关试题

