【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)

(1)到终点下车还有________人.
(2)车行驶在那两站之间车上的乘客最多?________站和________站
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式。
参考答案:
【答案】(1)29;(2)B;C;(3)150元.
【解析】
(1)根据正负数的意义,上车为正数,下车为负数,求出A、B、C、D站以及中点站的人数,即可得解;
(2)根据(1)的计算解答即可;
(3)根据各站之间的人数,乘以票价1元,然后计算即可得解
(1)根据题意可得:到终点前,车上有18+15-3+12-4+7-10+5-11=29,即29人;
故到终点下车还有29人.
(2)根据图表:易知B站和C站之间人数最多.
(3)根据题意:![]() (元).
(元).
故答案是:(1)29; (2)B,C; (3)150元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是 ( )
①若m=n,则|m|=|n|; ②若m=-n,则|m|=|-n|;
③若|-m|=|-n|,则m=-n; ④若|-m|=|-n|,则m=n.
A. ①② B. ③④ C. ①④ D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
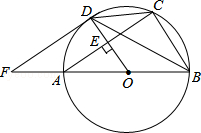
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是中国古代著名的“杨辉三角形”的示意图.图中填入的所有数的总和等于()

A. 126 B. 127 C. 128 D. 129
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P.
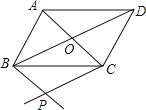
(1)判断四边形BPCO的形状,并说明理由;
(2)若将平行四边形ABCD改为菱形ABCD,其他条件不变,得到的四边形BPCO是什么四边形,并说明理由;
(3)若得到的是正方形BPCO,则四边形ABCD是 .(选填平行四边形、矩形、菱形、正方形中你认为正确的一个)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
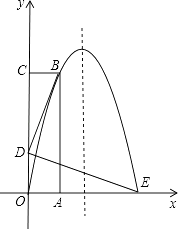
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标.
相关试题

