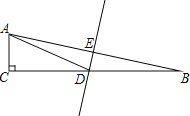
【题目】如图,在直角![]() 中,已知
中,已知![]() ,
,![]() 边的垂直平分线交
边的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长是________.
的长是________.
参考答案:
【答案】8
【解析】
根据直角三角形两锐角互余求得∠B的度数,利用线段垂直平分线的性质得AD=BD,利用等腰三角形的性质得∠DAE=∠B=15°,再利用外角的性质得∠ADC=30°,在三角形ADC中求出AD的长即可求得答案.
∵∠C=90°,∠BAC=75°,
∴∠B=90°-75°=15°,
∵AB边的垂直平分线交AB于E,交BC于D,,
∴AD=BD,
∴∠DAE=∠B=15°,
∴∠ADC=∠DAB+∠B=30°,
∴AC=![]() AD,
AD,
在Rt△ADC中,∠C=90°,由勾股定理得AD2=AC2+CD2,
即AD2=(![]() AD)2+(
AD)2+(![]() )2,
)2,
解得:AD=8,
∴BD=8,
故答案为:8.
-
科目: 来源: 题型:
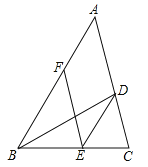
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球从起跑线
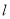 起跑,绕过
起跑,绕过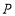 点跑回到起跑线(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果甲同学由于心急掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,甲同学说我俩所用的全部时间的和为50秒”,乙同学说捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问甲同学的速度是______米/秒.
点跑回到起跑线(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果甲同学由于心急掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,甲同学说我俩所用的全部时间的和为50秒”,乙同学说捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问甲同学的速度是______米/秒.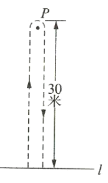
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
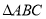 中,
中, 、
、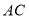 的垂直平分线
的垂直平分线 、
、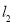 相交于点
相交于点 ,若
,若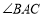 等于
等于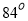 ,则
,则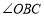 等于____________
等于____________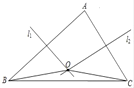
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
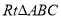 中,
中, ,
, ,BC=
,BC=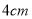 ,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为_________
,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读后,请解答.
已知
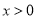 ,符合
,符合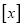 表示大于或等于
表示大于或等于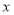 的最小正整数,如
的最小正整数,如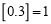 ,
,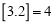 ,
,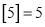 ,….
,….⑴填空:
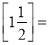 ________,
________,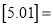 ________,若
________,若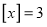 ,则
,则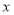 的取值范围是________.
的取值范围是________.⑵某市的出租车收费标准规定如下:
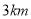 以内(包括
以内(包括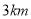 )收费
)收费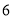 元,超过
元,超过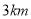 的每超过
的每超过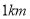 ,加收
,加收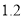 元(不足
元(不足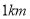 的按
的按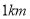 计算).用
计算).用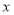 表示所行的千米数,
表示所行的千米数,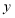 表示行
表示行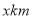 应付车费,则乘车费可按如下的公式计算:当
应付车费,则乘车费可按如下的公式计算:当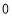 <
<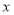 ≤
≤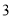 (单位:
(单位: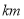 )时,
)时,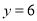 (元);当
(元);当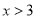 (单位:
(单位: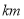 )时,
)时,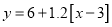 (元).某乘客乘车后付费
(元).某乘客乘车后付费 元,该乘客所行的路程
元,该乘客所行的路程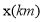 的取值范围是________.
的取值范围是________.
相关试题

