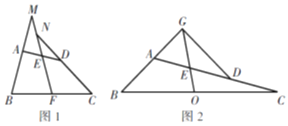
【题目】(1)如图1,在四边形ABCD中,F、E分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD;(提示取BD的中点H,连结FH,HE作辅助线)
(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.
参考答案:
【答案】(1)证明见解析;(2)OE=![]() .
.
【解析】
(1)连结BD,取DB的中点H,连结EH、FH,证明出EH∥AB,EH=![]() AB,FH∥CD,FH=
AB,FH∥CD,FH=![]() CD,证出HE=HF,进而证出AB=CD;
CD,证出HE=HF,进而证出AB=CD;
(2)连结BD,取DB的中点H,连结EH、OH,证明出HO=HE,可证明证出△OEH是等边三角形,进而求出OE=![]() .
.
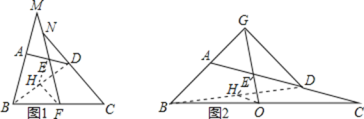
(1) 证明:如图一,连结BD,取DB的中点H,连结EH、FH.
∵E、F分别是AD、BC的中点,
∴EH∥AB,EH=![]() AB,FH∥CD,FH=
AB,FH∥CD,FH=![]() CD,
CD,
∵∠BME=∠CNE,
∴∠HEF=∠HFE,
∴HE=HF,
∴AB=CD;
(2) 如图二,连结BD,取DB的中点H,连结EH、OH,
∵AB=CD,HE为△ABD的中位线,HO为△BCD的中位线,
∴HO=HE=![]() AB=
AB=![]() CD,,
CD,,
∴∠HOE=∠HEO,
∵OH∥AC,∠OEC=60°,
∴∠OEH=∠HOE=∠OEC=60°,
∴△OEH是等边三角形,
∵AB=DC=5,
∴OE=![]() .
.
故答案为:(1)证明见解析;(2)OE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:

若学校在开学时要求每位学生在校一次性购买18个作业本,设x表示学生本学期使用作业本的数量,y表示购买作业本的费用(单位:元).
(1)写出x≤18和x>18时,y与x的函数关系式;
(2)在上述频数直方图中,当使用作业本的频率不小于0.5时,最少需要购买几个作业本;
(3)利用上述频数直方图,计算这30名学生平均使用作业本的费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】王警官骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,-8,+7,-15,+6,-16,+4,-2,+9.
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
-
科目: 来源: 题型:
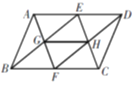
查看答案和解析>>【题目】如图,□ABCD中,E,F分别是AD,BC的中点,AF与BE交于点G,EC与DF交于点H,若GH=3,则AD=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户以1500元/亩的单价承包了15亩地种植板栗,每亩种植80株优质板栗嫁接苗,购买嫁接苗,购买价格为5元/株,且每亩地的管理费用为800元,一年下来喜获丰收平均每亩板栗产量为600kg,已知当地板栗的批发和;零售价格分别如下表所示:
销售方式
批发
零售
售价(元/kg)
10
14
通过市场调研发现,批发与零售的总销量只能达到总产量的70%,其中零售量不高于总销售量的40%,经多方协调当地食品加工厂承诺以7元/kg的价格收购该农户余下的板栗,设板栗全部售出后的总利润为y元,其中零售x kg.
(1)求y与x之间的函数关系
(2)求该农户所收获的最大利润
(总利润=总销售额-总承包费用-购买板栗苗的费用-总管理费用)
-
科目: 来源: 题型:
查看答案和解析>>【题目】空气质量状况已引起全社会的广泛关注,某市统计了2013年每月空气质量达到良好以上的天数,整理后制成如下折线统计图和扇形统计图.

根据以上信息解答下列问题:
(1)该市2013年每月空气质量达到良好以上天数的中位数是天,众数是天;
(2)求扇形统计图中扇形A的圆心角的度数;
(3)根据以上统计图提供的信息,请你简要分析该市的空气质量状况(字数不超过30字). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
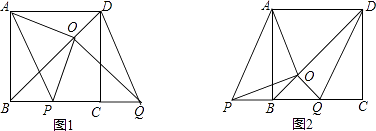
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB , BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
相关试题

