搜索
【题目】一个几何体及它的表面展开图如图所示．（几何体的上、下底面均为梯形）
（1）写出这个几何体的名称；
（2）计算这个几何体的侧面积和左视图的面积．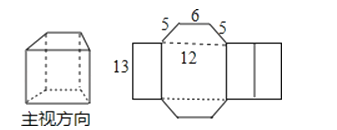
参考答案：
【答案】解：（1）观察图形可知，这个几何体是四棱柱；
（2）侧面积：13×（5+12+5+6）=13×28=364；
左视图的宽：（12﹣6）÷2=3，
=4，
左视图的面积：13×4=52．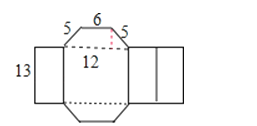
【解析】（1）根据几何体的三视图，可得出几何体是四棱柱；
（2）由图可得侧面积等于四个矩形的面积；左视图是一个长方形，根据勾股定理可得长方形的宽，再根据长方形的面积公式即可求解．
【考点精析】掌握由三视图判断几何体是解答本题的根本，需要知道在三视图中，通过主视图、俯视图可以确定组合图形的列数；通过俯视图、左视图可以确定组合图形的行数；通过主视图、左视图可以确定行与列中的最高层数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(12分)先阅读下面的例题，再按要求完成下列问题．
例：解不等式(x－2)(x＋1)＞0.
解：由有理数的乘法法则“两数相乘，同号得正”，得①
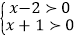或②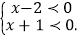
解不等式组①，得x＞2.
解不等式组②，得x＜－1.
所以不等式(x－2)(x＋1)＞0的解集为x＞2或x＜－1.
解不等式：(1)
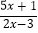＞0；(2) 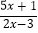＜0. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P是直线l外一点，A，B，C三点在直线l上，且PB⊥l于点B，∠APC＝90°，则下列结论：①线段AP是点A到直线PC的距离；②线段BP的长是点P到直线l的距离；③PA，PB，PC三条线段中，PB最短；④线段PC的长是点P到直线l的距离，其中，正确的是( )
A. ②③ B. ①②③ C. ③④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°．求∠APC度数．
小明的解题思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC=50°+60°=110°．
问题迁移：
（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．试判断∠CPD、∠α、∠β之间有何数量关系？请说明理由；
（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面直角坐标系中，△ABC的三个顶点坐标分别为A（0，4），B（3，4），C（4，﹣1）．
（1）试在平面直角坐标系中，画出△ABC；
（2）直接写出△ABC的面积_________
（3）若△A1B1C1与△ABC关于x轴对称，直接写出A1、B1、C1的坐标___________________________________
（4）在x轴上找到一点P，使点P到点A、B两点的距离和最小；
-
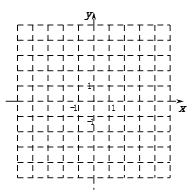
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，A、C、F、D在同一直线上，AF＝DC，AB∥DE，AB＝DE.
求证：(1) △ABC≌△DEF；
(2)BC∥EF.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）已知3x2-5x+1=0，求下列各式的值：①3x+
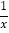；②9x2+
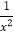；（2）若3xm+1-2xn-1+xn是关于x的二次多项式，试求3（m-n）2-4（n-m）2-（m-n）3+2（n-m）3的值．
相关试题
