【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC;
(2)直接写出△ABC的面积_________
(3)若△A1B1C1与△ABC关于x轴对称,直接写出A1、B1、C1的坐标___________________________________
(4)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
参考答案:
【答案】(1)图略(2)7.5(3)A1(0,-4),B1(3,-4)C1(4,1) (4)做A’(0,-4)连接A’B与x轴交点即为点P
【解析】
(1)根据题意作出图形即可;
(2)根据三角形的面积公式即可得到结论;
(3)根据关于x轴对称的点的特点即可得到结果;
(4)连接A1B交x轴于P即可得到结论.
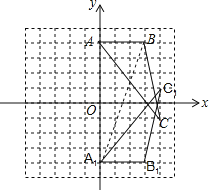
(1)如图所示△ABC即为所求;
(2)S△ABC=![]() ×3×5=
×3×5=![]() ;
;
(3)A1(0,-4),B1(3,-4),C1(4,1);
(4)连接A1B交x轴于P,点P即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直线l外一点,A,B,C三点在直线l上,且PB⊥l于点B,∠APC=90°,则下列结论:①线段AP是点A到直线PC的距离;②线段BP的长是点P到直线l的距离;③PA,PB,PC三条线段中,PB最短;④线段PC的长是点P到直线l的距离,其中,正确的是( )

A. ②③ B. ①②③ C. ③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体及它的表面展开图如图所示.(几何体的上、下底面均为梯形)
(1)写出这个几何体的名称;
(2)计算这个几何体的侧面积和左视图的面积.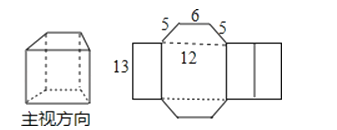
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,A、C、F、D在同一直线上,AF=DC,AB∥DE,AB=DE.
求证:(1) △ABC≌△DEF;
(2)BC∥EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知3x2-5x+1=0,求下列各式的值:①3x+
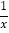 ;②9x2+
;②9x2+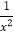 ;
;(2)若3xm+1-2xn-1+xn是关于x的二次多项式,试求3(m-n)2-4(n-m)2-(m-n)3+2(n-m)3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料.
让我们规定一种运算
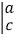
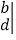 =ad-cb,如
=ad-cb,如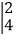
 =2×5-3×4=-2,再如
=2×5-3×4=-2,再如
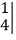 =4x-2.按照这种运算规定,请解答下列问题.
=4x-2.按照这种运算规定,请解答下列问题.(1)计算:
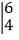
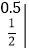 ;
;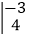
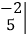 ;
;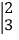
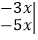 的值;
的值;(2)当x=-1时,求

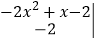 的值(要求写出计算过程).
的值(要求写出计算过程).
相关试题

