【题目】(1)已知3x2-5x+1=0,求下列各式的值:①3x+![]() ;②9x2+
;②9x2+![]() ;
;
(2)若3xm+1-2xn-1+xn是关于x的二次多项式,试求3(m-n)2-4(n-m)2-(m-n)3+2(n-m)3的值.
参考答案:
【答案】(1)①3x+![]() =5; ②9x2+
=5; ②9x2+![]() =19;(2)当m=1,n=2时,原式=2;当m=1,n=1时,原式=0;当m=0,n=2时,原式=20;当m=-1,n=2时,原式=72.
=19;(2)当m=1,n=2时,原式=2;当m=1,n=1时,原式=0;当m=0,n=2时,原式=20;当m=-1,n=2时,原式=72.
【解析】
(1)①根据3x2﹣5x+1=0,等式两边同除以x即可解答本题;
②根据①中的结果,两边同时平方,再化简即可解答本题;
(2)先化简所求式子,再根据3xm+1﹣2xn﹣1+xn是关于x的二次多项式,可以求得m、n的值,然后代入化简后的式子即可解答本题.
(1)①∵3x2﹣5x+1=0,∴3x﹣5![]() 0,∴3x
0,∴3x![]() 5;
5;
②∵3x![]() 5,∴
5,∴![]() ,∴
,∴![]() 25,∴
25,∴![]() 19;
19;
(2)3(m﹣n)2﹣4(n﹣m)2﹣(m﹣n)3+2(n﹣m)3
=﹣(m﹣n)2+3(n﹣m)3
∵3xm+1﹣2xn﹣1+xn是关于x的二次多项式,∴![]() 或
或![]() 或
或![]() 或
或![]() ,解得:
,解得:![]() 或
或![]() 或
或![]() 或
或![]() .
.
①当m=1,n=2时,原式=﹣(1﹣2)2+3(2﹣1)3=﹣1+3=2;
②当m=1,n=1时,原式=﹣(1﹣1)2+3(1﹣1)3=0;
③当m=0,n=2时,原式=﹣(0﹣2)2+3(2﹣0)3=﹣4+24=20;
④当m=﹣1,n=2时,原式=﹣(﹣1﹣2)2+3(2+1)3=﹣9+81=72.
综上所述:原式的值为2或0或20或72.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体及它的表面展开图如图所示.(几何体的上、下底面均为梯形)
(1)写出这个几何体的名称;
(2)计算这个几何体的侧面积和左视图的面积.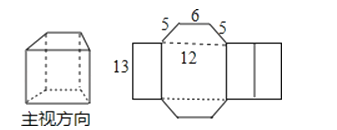
-
科目: 来源: 题型:
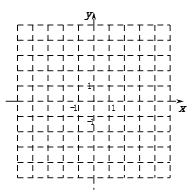
查看答案和解析>>【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC;
(2)直接写出△ABC的面积_________
(3)若△A1B1C1与△ABC关于x轴对称,直接写出A1、B1、C1的坐标___________________________________
(4)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,A、C、F、D在同一直线上,AF=DC,AB∥DE,AB=DE.
求证:(1) △ABC≌△DEF;
(2)BC∥EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料.
让我们规定一种运算
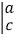
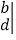 =ad-cb,如
=ad-cb,如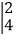
 =2×5-3×4=-2,再如
=2×5-3×4=-2,再如
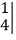 =4x-2.按照这种运算规定,请解答下列问题.
=4x-2.按照这种运算规定,请解答下列问题.(1)计算:
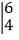
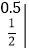 ;
;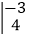
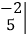 ;
;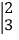
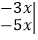 的值;
的值;(2)当x=-1时,求

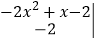 的值(要求写出计算过程).
的值(要求写出计算过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形BEFG平放在一起.
(1)若两正方形的面积分别是16和9,直接写出边AE的长为 .
(2)①设正方形ABCD的边长为a,正方形BEFG的边长为b,求图中阴影部分的面积(用含a和b的代数式表示)
②在①的条件下,如果a+b=10,ab=16,求阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个包装纸盒的三视图(单位:cm)
(1)该包装纸盒的几何形状是什么?
(2)画出该纸盒的平面展开图.
(3)计算制作一个纸盒所需纸板的面积.(精确到个位)
相关试题

