【题目】对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“结果是否>25?”为一次操作.
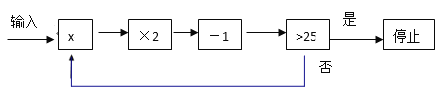
(1)如果操作只进行一次就停止,求x的取值范围;
(2)如果操作进行了四次才停止,求x的取值范围.
参考答案:
【答案】(1)x>13;(2)2.5<x≤4
【解析】
(1)表示出第一次输出结果,根据“操作只进行一次就停止”列不等式求解可得;
(2)表示出第一次、第二次、第三次、第四次的输出结果,再由第上次输出结果可得出不等式,解出即可.
(1)由已知得:2x-1>25,解得x>13.
故操作只进行一次就停止时,x的取值范围是x>13
(2)前四次操作的结果分别为:
2x-1,2(2x-1)-1=4x-3,2(4x-3)-1=8x-7,2(8x-7)-1=16x-15.
由已知得:![]() 解得2.5<x≤4.
解得2.5<x≤4.
故操作进行了四次才停止时,x的取值范围为2.5<x≤4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明租用共享单车从家出发,匀速骑行到相距2400米的邮局办事.小明出发的同时,他的爸爸以每分钟100米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
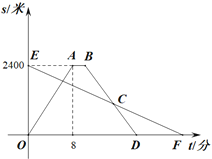
(1)求s1与t之间的函数表达式;
(2)小明从家出发,经过_______分在返回途中追上爸爸.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于
 的一元二次方程
的一元二次方程 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为 ,则另一个根为
,则另一个根为 ,因此
,因此 ,所以有
,所以有 ;我们记“
;我们记“ ”即
”即 时,方程
时,方程 为倍根方程;
为倍根方程;下面我们根据此结论来解决问题:
(1)方程①
 ;方程②
;方程② ;方程③
;方程③ 这几个方程中,是倍根方程的是_________(填序号即可);
这几个方程中,是倍根方程的是_________(填序号即可);(2)若
 是倍根方程,则
是倍根方程,则 的值为______;
的值为______; -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售樱桃,已知樱桃的进价为15元/千克,如果售价为20元/千克,那么每天可售出250千克,如果售价为25元/千克,那么每天可获利2000元,经调查发现:每天的销售量y(千克)与售价x(元/千克)之间存在一次函数关系.
(1)求y与x之间的函数关系式;
(2)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
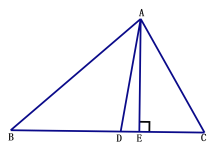
查看答案和解析>>【题目】如图,AD、AE分别是△ABC的角平分线和高线.
(1) 若∠B=50°,∠C=60°,求∠DAE的度数;
(2)若∠C >∠B,猜想∠DAE与∠C-∠B之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
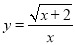 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数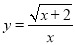 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:(1)函数
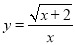 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;(2)下表是y与x的几组对应值.m的值为_______;
x
-2

-1
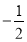
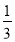
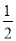
1
2
3
4
…
y
0
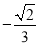
m
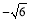
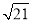
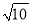
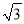
1
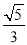
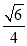
…
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:____________.
(5)结合函数图象估计
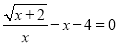 的解的个数为_______个.
的解的个数为_______个.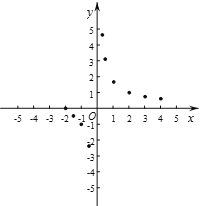
相关试题

