【题目】小明租用共享单车从家出发,匀速骑行到相距2400米的邮局办事.小明出发的同时,他的爸爸以每分钟100米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
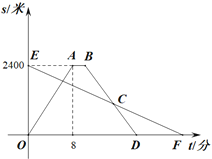
(1)求s1与t之间的函数表达式;
(2)小明从家出发,经过_______分在返回途中追上爸爸.
参考答案:
【答案】(1)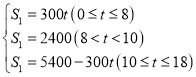 (2)15
(2)15
【解析】
(1)先根据图象可知:A(8,2400);B(10,2400);D(18,0),分3段列出解析式即可;
(2)根据E、F点的坐标求出EF所在的直线方程,求由BD与EF所在直线的交点即根据S1=S2列出方程求解即可.
解:(1)根据题意和图象可知:A(8,2400);B(10,2400);D(18,0),
当0≤t≤8时,设S1=kt,k=300,∴S1=300t;
当8<t<10时,S1=2400;
当10≤t≤18时,设S1=k1t+b,
将B、D点坐标代入得: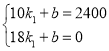
解得:![]()
∴S1=5400-300t
∴s1与t之间的函数表达式为: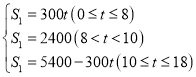
(2)∵2400÷100=24
∴点F的坐标为:(24,0)
设S2与t之间的函数表达式是S2=kt+b,则
![]() 解得:
解得:![]()
即S2与t之间的函数表达式是:S2=2400-100 t
根据题意列方程得:![]() ,
,
解得:t=15
∴小明从家出发,经过15分钟在返回途中追上爸爸.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点
 、点
、点 ,一次函数
,一次函数 的图象与直线AB交于点P.
的图象与直线AB交于点P.(1)求直线AB的函数表达式及P点的坐标;
(2)若点Q是y轴上一点,且△BPQ的面积为2,求点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?

-
科目: 来源: 题型:
查看答案和解析>>【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如下:
甲校学生样本成绩频数分布表
成绩m(分)
频数(人数)
频率

1
0.05

c
0.10
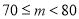
3
0.15

a
b

6
0.30
合计
20
1.0
表1

图1
b.甲校成绩在
 的这一组的具体成绩是:81 81 89 83 89 82 83 89
的这一组的具体成绩是:81 81 89 83 89 82 83 89c.甲、乙两校成绩的平均分、中位数、众数、方差如下:
学校
平均分
中位数
众数
方差
甲
84
n
89
129.7
乙
84.2
85
85
138.6
表2
根据以上图表提供的信息,解答下列问题:
(1)表1中a=______;表2中的中位数n =_______;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是84分,在他所属学校排在前10名,由表中数据可知该学生是______校的学生(填“甲”或“乙”),理由是________;
(4)假设甲校1000名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为_______人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于
 的一元二次方程
的一元二次方程 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为 ,则另一个根为
,则另一个根为 ,因此
,因此 ,所以有
,所以有 ;我们记“
;我们记“ ”即
”即 时,方程
时,方程 为倍根方程;
为倍根方程;下面我们根据此结论来解决问题:
(1)方程①
 ;方程②
;方程② ;方程③
;方程③ 这几个方程中,是倍根方程的是_________(填序号即可);
这几个方程中,是倍根方程的是_________(填序号即可);(2)若
 是倍根方程,则
是倍根方程,则 的值为______;
的值为______; -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“结果是否>25?”为一次操作.
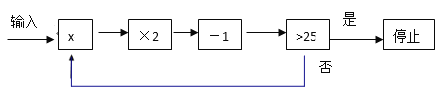
(1)如果操作只进行一次就停止,求x的取值范围;
(2)如果操作进行了四次才停止,求x的取值范围.
相关试题

