搜索
【题目】如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于( ).
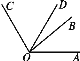
A. 50° B. 40° C. 30° D. 20°
参考答案：
【答案】B
【解析】
由题意，根据角平分线的性质可知∠AOD= ∠COD=
∠AOC ，根据角之间的等量关系∠BOC=2∠AOB ，∠BOC=∠COD+∠ BOD以及∠AOB=∠AOD- ∠BOD ，进行求解即可。
因为OD平分∠AOC ，所以∠COD =∠AOD =∠AOC ；又因为∠BOC=2∠AOB ，所以∠COD+∠BOD=2(∠AOD-∠BOD) ，所以3∠BOD=2 ∠AOD-∠COD =∠AOD =∠COD ；因为∠BOD=20°，所以∠AOB= ∠AOD- ∠BOD =2∠BOD =40°。
-
科目： 来源： 题型：
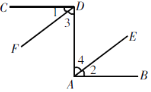
查看答案和解析>>【题目】如图，已知CD⊥DA，DA⊥AB，∠1=∠2. 试说明DF∥AE. 请你完成下列填空，把解答过程补充完整.
解：∵CD⊥DA，DA⊥AB，
∴∠CDA=90°，∠DAB=90°( ).
∴∠CDA=∠DAB(等量代换).
又∠1=∠2，
从而∠CDA-∠1=∠DAB-________(等式的性质).
即∠3=_______.
∴DF∥AE( ).
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，把直角三角形纸片沿过顶点B的直线（BE交CA于E）折叠，直角顶点C落在斜边AB上，如果折叠后得等腰△EBA，那么结论中：①∠A=30°；②点C与AB的中点重合；③点E到AB的距离等于CE的长，正确的个数是（ ）
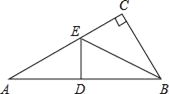
A. 0 B. 1 C. 2 D. 3
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程mx2﹣（2m﹣3）x+（m﹣1）=0有两个实数根．
（1）求m的取值范围；
（2）若m为正整数，求此方程的根． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线y=kx+b（k≠0）与双曲线y=
（m≠0）交于点A（2，﹣3）和点B（n，2）． 
（1）求直线与双曲线的表达式；
（2）对于横、纵坐标都是整数的点给出名称叫整点．动点P是双曲线y= （m≠0）上的整点，过点P作垂直于x轴的直线，交直线AB于点Q，当点P位于点Q下方时，请直接写出整点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=4，AC=6，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB、AC于M、N，则△AMN的周长为（ ）
A. 10 B. 6 C. 4 D. 不确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中正确的是（ ）
A. 若|a|=﹣a，则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1，次数是 6
C. 若 AP=BP，则点 P 是线段 AB 的中点
D. 若∠AOC=
∠AOB，则射线 OC 是∠AOB 的平分线
相关试题
