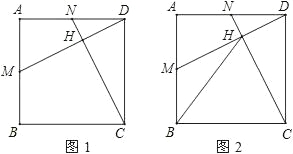
【题目】如图(1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)证明:①CN=DM;②CN⊥DM;
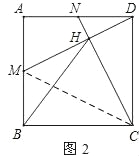
(2)设CN、DM的交点为H,连接BH,如图(2),求证:△BCH是等腰三角形.
参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、利用正方形的性质可求证△ADM≌△DCN,所以CN=DM,∠ADM=∠DCN,∠ADM+∠CDM=∠DCN+∠CDM=90°,即可求证∠CHD=90°;(2)、连接CM,易证M、B、C、H四点共圆,所以∠BMC=∠BHC,证明△AMD≌△BCM,即可求证∠BHC=∠BCH
试题解析:(1)、由题意知:AD=CD, ∵M、N分别是AB和AD的中点, ∴AM=DN,
在△ADM与△DCN中,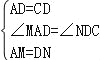 , ∴△ADM≌△DCN(SAS), ∴DM=CN,∠ADM=∠DCN,
, ∴△ADM≌△DCN(SAS), ∴DM=CN,∠ADM=∠DCN,
∴∠DCN+∠CDM=∠ADM+∠CDM=90°, ∴∠CHD=90°, ∴CN⊥DM;
(2)、连接CM, 由(1)可知:∠AMD=90°﹣∠ADM, ∠BCH=90°﹣∠DCN, ∴∠AMD=∠BCH,
∴M、B、C、H四点共圆, ∴∠BMC=∠BHC,
在△BCM与△ADM中,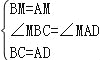 , ∴△BCM≌△ADM(SAS), ∴∠BMC=∠AMD,
, ∴△BCM≌△ADM(SAS), ∴∠BMC=∠AMD,
∴∠BHC=∠AMD=∠BCH, ∴△BCH是等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点F是CD 的中点,且AF⊥CD,BC=ED,∠BCD=∠EDC.
(1)求证:BF=EF;
(2)求证:AB=AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 , 数轴上表示2和﹣3的两点之间的距离是
(2)数轴上表示x和﹣2的两点之间的距离表示为 .
(3)若x表示一个有理数,且﹣4≤x≤﹣2,则|x﹣2|+|x+4|=
(4)若|x+3|+|x﹣5|=8,利用数轴求出x的整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣ ×[﹣32×(﹣
×[﹣32×(﹣  )2﹣2]÷(﹣1)2006
)2﹣2]÷(﹣1)2006
(2)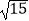 ﹣
﹣ 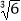 (结果精确到0.1)
(结果精确到0.1)
(3)﹣22﹣(﹣1)5×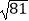
(4)﹣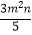 +m2n﹣mn2
+m2n﹣mn2
(5)2(x﹣1)﹣3(2﹣3x) -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形从一个顶点,只可以引三条对角线,则它是( )边形.
A. 五 B. 六 C. 七 D. 八
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则下列各式中正确的是( )
A.a﹣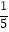 <b﹣
<b﹣ 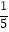
B.﹣4a>﹣4b
C.﹣2a+1<﹣2b+1
D.a2>b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的边数增加1,那么它的内角和增加( ).
A. 0° B. 90° C. 180° D. 360°
相关试题

