【题目】如图,点F是CD 的中点,且AF⊥CD,BC=ED,∠BCD=∠EDC.
(1)求证:BF=EF;
(2)求证:AB=AE.

参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据中点定义可得CF=DF,然后证明△BCF≌△EDF,进而可得FB=FE;(2)、根据△BCF≌△EDF可得FB=EF,∠BFC=∠EFD,再证明∠BFA=∠EFA,然后判定△ABF≌△AEF可得AB=AE.
试题解析:(1)、∵点F是CD 的中点, ∴CF=DF,
在△BCF和△EDF中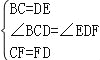 , ∴△BCF≌△EDF(SAS), ∴FB=FE;
, ∴△BCF≌△EDF(SAS), ∴FB=FE;
(2)、∵△BCF≌△EDF, ∴FB=EF,∠BFC=∠EFD, ∵AF⊥CD, ∴∠BFC+∠AFB=∠AFE+∠EFD,
∴∠BFA=∠EFA, 在△ABF和△AEF中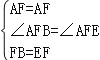 , ∴△ABF≌△AEF(SAS), ∴AB=AE.
, ∴△ABF≌△AEF(SAS), ∴AB=AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人连续7年调查某县养鸡业的情况,提供了如下两方面的信息图:

甲调查表明:养鸡场的平均产鸡数从第1年的1万只上升到第7年的2.8万只;
乙调查表明:养鸡场的个数由第1年的46个减少到第7年的22个.
现在给出下列四个判断:(1)该县第2年养鸡场产鸡的数量为1.3万只;(2)该县第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量;(3)该县这7年养鸡场产鸡的数量逐年增长;(4)在这7年中,第5年该县养鸡场产鸡的数量最多.
根据甲、乙两人提供的信息,可知其中正确的判断有( ).
A. 3个 B. 2个 C. 1 个 D. 0 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一条边长为7,另一边长为15,则它的周长为____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)
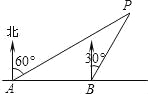
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 , 数轴上表示2和﹣3的两点之间的距离是
(2)数轴上表示x和﹣2的两点之间的距离表示为 .
(3)若x表示一个有理数,且﹣4≤x≤﹣2,则|x﹣2|+|x+4|=
(4)若|x+3|+|x﹣5|=8,利用数轴求出x的整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣ ×[﹣32×(﹣
×[﹣32×(﹣  )2﹣2]÷(﹣1)2006
)2﹣2]÷(﹣1)2006
(2)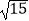 ﹣
﹣ 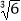 (结果精确到0.1)
(结果精确到0.1)
(3)﹣22﹣(﹣1)5×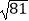
(4)﹣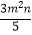 +m2n﹣mn2
+m2n﹣mn2
(5)2(x﹣1)﹣3(2﹣3x) -
科目: 来源: 题型:
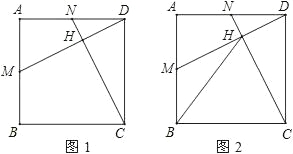
查看答案和解析>>【题目】如图(1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)证明:①CN=DM;②CN⊥DM;
(2)设CN、DM的交点为H,连接BH,如图(2),求证:△BCH是等腰三角形.
相关试题

