搜索
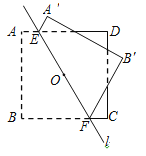
【题目】如图，正方形ABCD的边长为2，点O是正方形的中心，过点O作一条直线l分别交正方形AD，BC两边于点E，F.直线l将正方形分成两部分，将其中的一个部分沿这条直线翻折到另一个部分上，若AE＝
，则两个部分图形中不重叠部分的面积为_______．
参考答案：
【答案】12－8
【解析】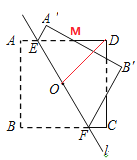
连接OD，因点O是正方形的中心，可求得OD=
，∠ODE=45° ，因AE＝2-
，正方形的边长是2，可求得DE=
，即可得OD=DE，根据等腰三角形的性质和三角形的内角和定理可得∠DEA=67.5°，根据对顶角相等和折叠的性质可得∠AEA’=135°，所以∠AEM=45°，△AEM是等腰直角三角形，根据条件易证这两个部分图形中不重叠部分的四个等腰直角三角形全等，即可得这两个部分图形中不重叠部分的面积为
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若关于x的方程x2+3x+a=0有一个根为﹣1，则a的值为（ ）
A.2
B.﹣1
C.﹣2
D.1 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D，连接AC，BD，CD.
(1)求点C，D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q，连接QA，QB，使S△QAB＝S四边形ABDC？若存在这样一点，求出点Q的坐标；若不存在，试说明理由．
(3)如图②，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时(不与B，D重合)，给出下列结论：①
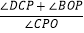的值不变，②
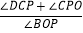的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．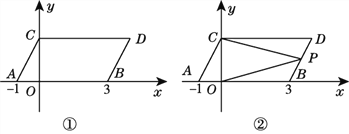
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O直径，OD⊥弦BC与点F，且交⊙O于点E，且∠AEC＝∠ODB．
（1）判断直线BD和⊙O的位置关系，并给出证明；
（2）当tan∠AEC=
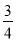，BC＝8时，求OD的长．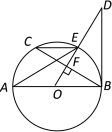
-
科目： 来源： 题型：
查看答案和解析>>【题目】把抛物线y＝x2先向左平移1个单位长度，再向下平移3个单位长度，得到新的抛物线解析式为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将y=x2向上平移2个单位后所得到的抛物线的解析式为（ ）
A.y=x2﹣2
B.y=x2+2
C.y=（x﹣2）2
D.y=（x+2）2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AC平分∠DAE，DA∥CE，AB=CB．
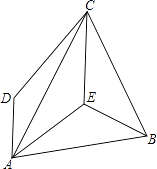
（1）试判断BE与AC有何位置关系？并证明你的结论；
（2）若∠DAC=25°，求∠AEB的度数．
相关试题
