【题目】如图,⊙A,⊙B的半径分别为1cm,2cm,圆心距AB为5cm.如果⊙A由图示位置沿直线AB向右平移2cm,则此时该圆与⊙B的位置关系是( )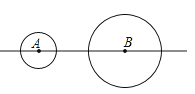
A.外离
B.相交
C.外切
D.内含
参考答案:
【答案】C
【解析】解答:∵圆心距AB是5cm,把⊙A由图示位置沿直线AB向右平移2cm,
∴新的圆心距AB是5-2=3cm,
又∵⊙A和⊙B的半径分别是1cm和2cm,则2-1=1,2+1=3,
∴两圆恰好外切.故选C.
求出把⊙A由图示位置沿直线AB向右平移2cm后,⊙A和⊙B的圆心距,再求出两圆半径的和与差,与该圆心距进行比较,确定两圆的位置关系.
【考点精析】认真审题,首先需要了解圆与圆的位置关系(两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( )

A.3次
B.4次
C.5次
D.6次 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
 (k>0)与一次函数
(k>0)与一次函数 的图象相交于两点A(
的图象相交于两点A( ,
, ),B(
),B( ,
, ),线段AB交y轴与C,当|
),线段AB交y轴与C,当| -
- |=2且AC = 2BC时,k、b的值分别为( )
|=2且AC = 2BC时,k、b的值分别为( )
A. k=
 ,b=2 B. k=
,b=2 B. k= ,b=1 C. k=
,b=1 C. k= ,b=
,b= D. k=
D. k= ,b=
,b=
【答案】D
【解析】∵AC=2BC,∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.∵点A、点B都在一次函数y=x+b的图象上,∴设B(m,
 m+b),则A(-2m,-m+b),∵|
m+b),则A(-2m,-m+b),∵| -
- |=2,∴m-(-2m)=2,解得m=
|=2,∴m-(-2m)=2,解得m= ,又∵点A、点B都在反比例函数
,又∵点A、点B都在反比例函数 的图象上,∴
的图象上,∴ (
( +b)=(-
+b)=(- )×(-
)×(- +b),解得b=
+b),解得b= ,∴k=
,∴k= ×(
×( +
+ )=
)= ,故选D.
,故选D.【题型】单选题
【结束】
11【题目】若点(4,m)在反比例函数
 (x≠0)的图象上,则m的值是 .
(x≠0)的图象上,则m的值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若点(4,m)在反比例函数
 (x≠0)的图象上,则m的值是 .
(x≠0)的图象上,则m的值是 .【答案】2
【解析】∵点(4,m)在反比例函数y=
 (x≠0)的图象上,
(x≠0)的图象上,∴m=8÷4,解得m=2.
故答案为:2.
【题型】填空题
【结束】
12【题目】如上图,反比例函数
 的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .
的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE
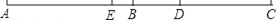
(1)若AB=18,BC=21,求DE的长;
(2)若AB=a,求DE的长;(用含a的代数式表示)
(3)若图中所有线段的长度之和是线段AD长度的7倍,则
 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如上图,反比例函数
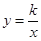 的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .
的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .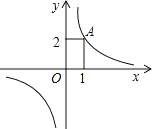
【答案】(-1,-2)(答案不唯一).
【解析】试题分析:根据“第一象限内的图象经过点A(1,2)”先求出函数解析式,给x一个值负数,求出y值即可得到坐标.
试题解析:∵图象经过点A(1,2),
∴
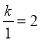
解得k=2,
∴函数解析式为y=
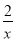 ,
,当x=-1时,y=
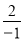 =-2,
=-2,∴P点坐标为(-1,-2)(答案不唯一).
考点:反比例函数图象上点的坐标特征.
【题型】填空题
【结束】
13【题目】在y轴右侧且平行于y轴的直线l被反比例函数
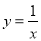 (
(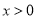 )与函数
)与函数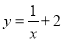 (
(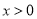 )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位. 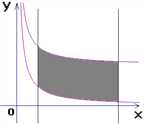
相关试题

