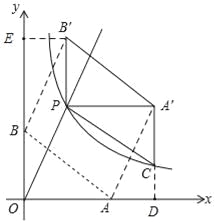
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

参考答案:
【答案】(1)k1=2,k2=8;(2)![]() ;(3)22
;(3)22
【解析】试题分析:(1)把点P(2,4)代入直线y=k1x,把点P(2,4)代入双曲线y=![]() ,可得k1与k2的值;
,可得k1与k2的值;
(2)根据平移的性质,求得C(6,![]() ),再运用待定系数法,即可得到直线PC的表达式;
),再运用待定系数法,即可得到直线PC的表达式;
(3)延长A'C交x轴于D,过B'作B'E⊥y轴于E,根据△AOB≌△A'PB',可得线段AB扫过的面积=平行四边形POBB'的面积+平行四边形AOPA'的面积,据此可得线段AB扫过的面积.
试题解析:(1)把点P(2,4)代入直线y=k1x,可得4=2k1,
∴k1=2,
把点P(2,4)代入双曲线y=![]() ,可得k2=2×4=8;
,可得k2=2×4=8;
(2)∵A(4,0),B(0,3),
∴AO=4,BO=3,
如图,延长A'C交x轴于D,
由平移可得,A'P=AO=4,
又∵A'C∥y轴,P(2,4),
∴点C的横坐标为2+4=6,
当x=6时,y=![]() =
=![]() ,即C(6,
,即C(6,![]() ),
),
设直线PC的解析式为y=kx+b,
把P(2,4),C(6,![]() )代入可得
)代入可得
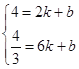 ,解得
,解得 ,
,
∴直线PC的表达式为y=﹣![]() x+
x+![]() ;
;
(3)如图,延长A'C交x轴于D,
由平移可得,A'P∥AO,
又∵A'C∥y轴,P(2,4),
∴点A'的纵坐标为4,即A'D=4,
如图,过B'作B'E⊥y轴于E,
∵PB'∥y轴,P(2,4),
∴点B'的横坐标为2,即B'E=2,
又∵△AOB≌△A'PB',
∴线段AB扫过的面积=平行四边形POBB'的面积+平行四边形AOPA'的面积=BO×B'E+AO×A'D=3×2+4×4=22.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.
(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?
(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出的两个都是蜜枣粽的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(﹣1)﹣3=1
B.(﹣4)0=1
C.(﹣2)2×(﹣2)﹣3=26
D.2a﹣4=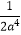
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(2,m),B(n,﹣5),根据下列条件求m,n的值.
(1)A,B两点关于y轴对称;
(2)AB∥y轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C1:y=ax2﹣4ax﹣5(a>0).
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列代数运算正确的是( )
A.2﹣3=﹣8
B.(2x2)3=8x6
C.x6÷x2=x3
D.x2+x3=2x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0),其中自变量x与函数值y之间满足下面的对应关系:
x
…
3
5
7
…
y
…
2.5
2.5
﹣1.5
…
则a+b+c=_____.
相关试题

