搜索
【题目】已知点A（2，m），B（n，﹣5），根据下列条件求m，n的值．
（1）A，B两点关于y轴对称；
（2）AB∥y轴．
参考答案：
【答案】（1）m=﹣5，n=﹣2；（2）m≠﹣5，n=2
【解析】
（1）根据关于y轴对称的点的坐标的特点是：横坐标互为相反数，纵坐标不变，即可求出m、n的值；
（2）根据平行线的性质：平行于y轴的所有点的横坐标相等即可得出答案．
（1）根据轴对称的性质，得m=﹣5，n=﹣2；
（2）根据平行线的性质，得m≠﹣5，n=2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们定义：如图1，在△ABC看，把AB点绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC'，连接B'C'．当α+β=180°时，我们称△A'B'C'是△ABC的“旋补三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．
特例感知：
（1）在图2，图3中，△AB'C'是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．
①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD= BC；
②如图3，当∠BAC=90°，BC=8时，则AD长为 ．
猜想论证：
（2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．
拓展应用
（3）如图4，在四边形ABCD，∠C=90°，∠D=150°，BC=12，CD=2
，DA=6．在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，给予证明，并求△PAB的“旋补中线”长；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】端午节那天，小贤回家看到桌上有一盘粽子，其中有豆沙粽、肉粽各1个，蜜枣粽2个，这些粽子除馅外无其他差别．
（1）小贤随机地从盘中取出一个粽子，取出的是肉粽的概率是多少？
（2）小贤随机地从盘中取出两个粽子，试用画树状图或列表的方法表示所有可能的结果，并求出小贤取出的两个都是蜜枣粽的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）
A.（﹣1）﹣3=1
B.（﹣4）0=1
C.（﹣2）2×（﹣2）﹣3=26
D.2a﹣4=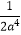
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝k1x(x≥0)与双曲线y＝
(x＞0)相交于点P(2，4)．已知点A(4，0)，B(0，3)，连接AB，将Rt△AOB沿OP方向平移，使点O移动到点P，得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C，连接CP.(1)求k1与k2的值；
(2)求直线PC的解析式；
(3)直接写出线段AB扫过的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线C1：y=ax2﹣4ax﹣5（a＞0）．
（1）当a=1时，求抛物线与x轴的交点坐标及对称轴；
（2）①试说明无论a为何值，抛物线C1一定经过两个定点，并求出这两个定点的坐标；
②将抛物线C1沿这两个定点所在直线翻折，得到抛物线C2，直接写出C2的表达式；
（3）若（2）中抛物线C2的顶点到x轴的距离为2，求a的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列代数运算正确的是（ ）
A.2﹣3=﹣8
B.（2x2）3=8x6
C.x6÷x2=x3
D.x2+x3=2x5
相关试题
