【题目】已知如图,四边形![]() 中,
中,![]() 于点
于点![]() ,
,![]() .点
.点![]() 为
为![]() 边上一点,以
边上一点,以![]() 为边作平行四边形
为边作平行四边形![]() ,则
,则![]() 最小值是__________.
最小值是__________.

参考答案:
【答案】4
【解析】
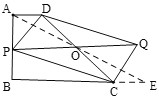
设对角线PQ与DC相交于点O,连接AO并延长AO交BC的延长线于E,根据平行四边形得性质可知点O为CD、PQ的中点,根据平行线的性质可得∠DAE=∠E,利用AAS可证明△AOD≌△EOC,可得AD=CE,可求出BE的长,由垂线段最短可知当OP⊥AB时,OP最短,可得PQ为最小值,由AB⊥BC,可得OP//BC,由OD=OC可得OP为△ABE的中位线,根据三角形中位线的性质可求出OP的长,进而可求出PQ的长.
如图,设对角线PQ与DC相交于点O,连接AO并延长AO交BC的延长线于E,
∵四边形![]() 是平行四边形,
是平行四边形,
∴O是DC、PQ的中点,即OD=OC,OP=OQ,
∵![]()
∴∠DAE=∠E,
在△AOD和△EOC中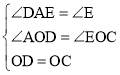 ,
,
∴△AOD≌△EOC(AAS),
∴![]() ,
,
∵AD=1,BC=3,
∴BE=4,
当OP⊥AB时,OP最短,即PQ有最小值,
∵AB⊥BC,AD//BC,
∴OP//AD//BC,
∴OP为△ABE的中位线,
∴OP=![]() BE=2,
BE=2,
∴PQ=2OP=4,即PQ的最小值为4,
故答案为:4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,0),B(0,4),C(3,t+4),D(3,t). 记N(t)为
 ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为A. 6、7B. 7、8C. 6、7、8D. 6、8、9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2 , 且满足x12+x22=10,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=84°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠P=100°,则∠ACB的大小为__________

-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的
 (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在要生产甲乙两种产品,甲产品需要A原料15千克,B原料20千克 ;乙产品需要A原料20千克,B原料10千克.现在A原料有360千克,B原料300千克.现在要生产甲乙两种产品共20件.
(1)共有几种方案
(2)已知生产甲产品成本是每件10元,乙产品成本每件8元.那么生产多少件甲产品可以使生产成本最低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,点
中,点 为直角坐标系的原点,
为直角坐标系的原点, 的坐标分别为
的坐标分别为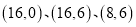 .点
.点 同时从原点出发,分别作匀速运动,点
同时从原点出发,分别作匀速运动,点 沿
沿 以每秒1个单位向终点
以每秒1个单位向终点 运动,点
运动,点 沿
沿 以每秒2个单位向终点
以每秒2个单位向终点 运动.当这两点中有一点到达自己的终点时,另一点也停止运动.设运动时间为
运动.当这两点中有一点到达自己的终点时,另一点也停止运动.设运动时间为 秒.
秒.
(1)请用
 表示点
表示点 的坐标为__________;
的坐标为__________;(2)是否存在某个时间
 ,使得以点
,使得以点 和四边形
和四边形 中的任意两个顶点为顶点的四边形为平行四边形?若存在,请求出
中的任意两个顶点为顶点的四边形为平行四边形?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

