【题目】已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2 , 且满足x12+x22=10,求实数m的值.
参考答案:
【答案】
(1)解:∵方程x2﹣2(m+1)x+m2+2=0有实数根,
∴△=[﹣2(m+1)]2﹣4(m2+2)=8m﹣4≥0,
解得:m≥ ![]()
(2)解:∵方程x2﹣2(m+1)x+m2+2=0的两实数根分别为x1、x2,
∴x1+x2=2(m+1),x1x2=m2+2,
∴x12+x22= ![]() ﹣2x1x2=[2(m+1)]2﹣2(m2+2)=2m2+8m=10,
﹣2x1x2=[2(m+1)]2﹣2(m2+2)=2m2+8m=10,
解得:m1=﹣5(舍去),m2=1.
∴实数m的值为1
【解析】(1)根据方程有实数根,得出△≥0,建立不等式,求出解集即可;
(2)利用根与系数的关系,求出方程的两根之和及两根之积。再根据x12+x22=10,,建立方程,求出方程的解,再根据(1)中,m的取值范围确定出m的值。
【考点精析】解答此题的关键在于理解因式分解法的相关知识,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势,以及对求根公式的理解,了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,求∠HPQ的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据语句画图,并回答问题,如图,∠AOB内有一点P.
(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D.
(2)写出图中与∠CPD互补的角 .(写两个即可)
(3)写出图中∠O相等的角 .(写两个即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,0),B(0,4),C(3,t+4),D(3,t). 记N(t)为
 ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为A. 6、7B. 7、8C. 6、7、8D. 6、8、9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=84°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠P=100°,则∠ACB的大小为__________

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,四边形
 中,
中,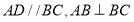 于点
于点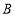 ,
, .点
.点 为
为 边上一点,以
边上一点,以 为边作平行四边形
为边作平行四边形 ,则
,则 最小值是__________.
最小值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的
 (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
相关试题

