【题目】如图,在平面直角坐标系xOy中,直线y=﹣2x+a与y轴交于点C (0,6),与x轴交于点B.

(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(﹣1,n),点A的坐标为(﹣3,0).
①求n的值及直线AD的解析式;
②求△ABD的面积;
③点M是直线y=﹣2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
参考答案:
【答案】(1)y=﹣2x+6(2)①y=4x+12 ②24 ③S=6m-18.
【解析】试题分析:(1)利用待定系数法可求函数的解析式;
(2)①根据题意直接代入函数的解析式求出n,得到D点的坐标,然后由A、D点的坐标,由待定系数法求出AD的解析式;
②构造三角形直接求面积;
③由点M在直线y=-2x+6得到M的坐标,构造三角形,然后分类求解即可.
试题解析:(1)∵直线y=﹣2x+a与y轴交于点C (0,6),∴a=6,
∴该直线解析式为y=﹣2x+6.

(2)①∵点D(﹣1,n)在直线BC上,
∴n=﹣2×(﹣1)+6=8,
∴点D(﹣1,8).
设直线AD的解析式为y=kx+b,
将点A(﹣3,0)、D(﹣1,8)代入y=kx+b中,
得:![]() ,解得:
,解得:![]() ,
,
∴直线AD的解析式为y=4x+12.
②令y=﹣2x+6中y=0,则﹣2x+6=0,解得:x=3,∴点B(3,0).
∵A(﹣3,0)、D(﹣1,8),∴AB=6.
S△ABD=![]() AByD=
AByD=![]() ×6×8=24
×6×8=24
③∵点M在直线y=-2x+6上,∴M(m,-2m+6),
![]()
当m<3时,S=![]()
即![]() ;
;
当m>3时, ![]()
即S=6m-18.
-
科目: 来源: 题型:
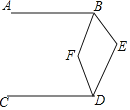
查看答案和解析>>【题目】如图,
 平分
平分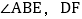 平分
平分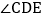 ,则
,则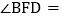 ______ .
______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
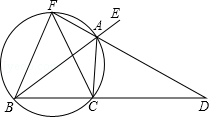
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截,在下面三个式子只,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并写出对应的推理过程
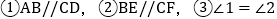 题设
题设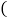 已知
已知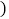 ;______
;______ 结论
 求证
求证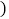 :______
:______ 理由:
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3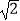 时,求线段DH的长.
时,求线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,纸片
 ABCD中,AD=5,
ABCD中,AD=5,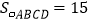 ,过点A作AE⊥BC,垂足为E,沿AE剪下
,过点A作AE⊥BC,垂足为E,沿AE剪下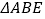 ,将它平移至
,将它平移至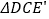 的位置,拼成四边形
的位置,拼成四边形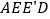 ,则四边形
,则四边形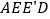 的形状为(_____)
的形状为(_____)A.平行四边形 B.菱形 C.矩形 D.正方形
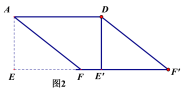
(2)如图2,在(1)中的四边形
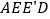 中,在EF上取一点P,EP=4,剪下
中,在EF上取一点P,EP=4,剪下 ,将它平移至
,将它平移至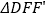 的位置,拼成四边形
的位置,拼成四边形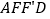 。①求证:四边形
。①求证:四边形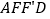 是菱形;②求四边形
是菱形;②求四边形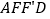 的两条对角线的长。
的两条对角线的长。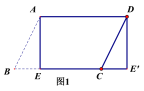
相关试题

