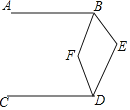
【题目】如图,![]() 平分
平分![]() 平分
平分![]() ,则
,则![]() ______ .
______ .
参考答案:
【答案】![]()
【解析】
首先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的性质,即可求得∠ABF+∠CDF的度数,又由两只线平行,内错角相等,即可求得∠BFD的度数.
过点E作EM∥AB,过点F作FN∥AB,
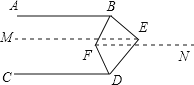
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() (∠ABE+∠CDE)=125°,
(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故答案为125°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
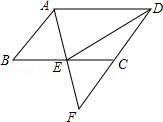
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:
 有公共顶点和一条公共边的两个角一定是邻补角;
有公共顶点和一条公共边的两个角一定是邻补角; 垂线段最短;
垂线段最短; 经过直线外一点,有且只有一条直线与这条直线平行;
经过直线外一点,有且只有一条直线与这条直线平行; 相等的角是对顶角;
相等的角是对顶角; 等角的余角相等,其中假命题的个数是
等角的余角相等,其中假命题的个数是
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB‖CD,∠EAF =
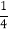 ∠EAB,∠ECF=
∠EAB,∠ECF=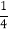 ∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________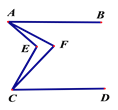
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
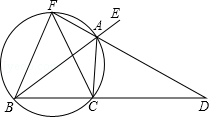
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截,在下面三个式子只,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并写出对应的推理过程
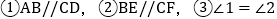 题设
题设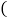 已知
已知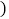 ;______
;______ 结论
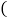 求证
求证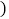 :______
:______ 理由:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣2x+a与y轴交于点C (0,6),与x轴交于点B.

(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(﹣1,n),点A的坐标为(﹣3,0).
①求n的值及直线AD的解析式;
②求△ABD的面积;
③点M是直线y=﹣2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
相关试题

