Question

【题目】如图，△ABC中，∠ACB=90°，AC=BC，在△ABC外侧作直线CP，点A关于直线CP的对称点为D，连接AD，BD，其中BD交直线CP于点E．

（1）如图1，∠ACP=15°．

①依题意补全图形；

②求∠CBD的度数；

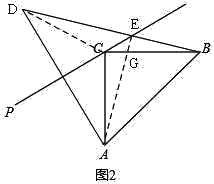
（2）如图2，若45°＜∠ACP＜90°，直接用等式表示线段AC，DE，BE之间的数量关系．

Answer 1

【答案】（1）①见解析；②30°；（2）DE2+BE2=2AC2，理由见解析

【解析】

（1）根据题意作图，进而求∠CBD的度数（2）由45°＜∠ACP＜90°，根据题意和图形可得DE2+BE2=2AC2 .

（1）如图1所示，

（2）如图1，连接CD，

∵点A关于直线CP的对称点为D，

∴CP是AD的垂直平分线，

∴CD=AC，∠DCP=∠ACP=15°，

∵∠ACB=90°，

∴∠BCD=90°+15°+15°=120°，

∵AC=BC=CD，

∴∠CBD=∠CDB=30°，

（3）DE2+BE2=2AC2，

理由是：如图2，连接CD、AE，

∵DC=BC=AC，

∴∠CDB=∠CBD=∠CAE，

∵∠CGA=∠EGB，

∴∠GEB=∠ACB=90°，

∴AE2+BE2=AB2，

∵CP是AD的垂直平分线，

∴ED=AE，

∴DE2+BE2=AB2，

∵△ABC是等腰直角三角形，

∴AB2=AC2+BC2，且AC=BC，

∴DE2+BE2=2AC2．