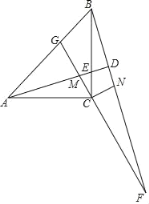
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点E是BC上一点(不与点B,C重合),点M是AE上一点(不与点A,E重合),连接并延长CM交AB于点G,将线段CM绕点C按顺时针方向旋转90°,得到线段CN,射线BN分别交AE的延长线和GC的延长线于D,F.
(1)求证:△ACM≌△BCN;
(2)求∠BDA的度数;
(3)若∠EAC=15°,∠ACM=60°,AC=![]() +1,求线段AM的长.
+1,求线段AM的长.
参考答案:
【答案】(1)见解析;(2)∠BDA=90°;(3)AM=![]() .
.
【解析】
(1)根据题意可知∠ACM=∠BCN,再利用SAS即可证明
(2)根据(1)可求出∠ACE=∠BDE=90°,即可解答
(3)作MH⊥AC交AC于H.在AC上取一点,使得AQ=MQ,设EH=a.可知AQ=QM=2a,QH=![]() a,再求出a的值,利用勾股定理即可解答
a,再求出a的值,利用勾股定理即可解答
(1)∵∠ACB=90°,∠MCN=90°,
∴∠ACM=∠BCN,
在△MAC和△NBC中
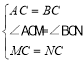 ,
,
∴△MAC≌△NBC(SAS).
(2)∵△MAC≌△NBC,
∴∠NBC=∠MAC
∵∠AEC=∠BED,
∴∠ACE=∠BDE=90°,
∴∠BDA=90°.
(3)作MH⊥AC交AC于H.在AC上取一点,使得AQ=MQ,设EH=a.
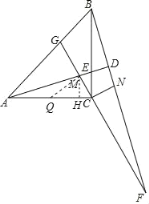
∵AQ=QM,
∴∠QAE=∠AMQ=15°,
∴∠EQH=30°,
∴AQ=QM=2a,QH=![]() a,
a,
∵∠ECH=60°,
∴CH=![]() a,
a,
∵AC=![]() +1,
+1,
∴2a+![]() a+a=
a+a=![]() +1,
+1,
∴a=![]() ,
,
∵AM=![]() =(
=(![]() +
+![]() )a=
)a=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解全校学生下学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
活动次数x
频数
频率
0<x≤3
10
0.20
3<x≤6
a
0.24
6<x≤9
16
0.32
9<x≤12
m
b
12<x≤15
4
0.08
15<x≤18
2
n

根据以上图表信息,解答下列问题:
(1)表中a=___,b=___;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1500名学生,请估计该校在下学期参加社区活动超过6次的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
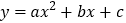 (a、b、c是常数,
(a、b、c是常数,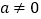 )的对称轴为直线
)的对称轴为直线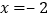 .
.(1) b=______;(用含a的代数式表示)
(2)当
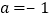 时,若关于x的方程
时,若关于x的方程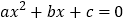 在
在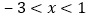 的范围内有解,求c的取值范围;
的范围内有解,求c的取值范围;(3)若抛物线过点(
 ,
, ),当
),当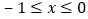 时,抛物线上的点到x轴距离的最大值为4,求a的值.
时,抛物线上的点到x轴距离的最大值为4,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,∠B=90°,DC=5cm.点P从点A向点D以lcm/s的速度运动,到D点停止,点Q从点C向B点以2cm/s的速度运动,到B点停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP= ;BQ= .
(2)当t为何值时,四边形PDCQ是平行四边形?
(3)当t为何值时,△QCD是直角三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解成都市初中学生“数学核心素养”的掌握情况,教育科学院命题教师赴某校初三年级进行调 研,命题教师将随机抽取的部分学生成绩(得分为整数,满分 160 分)分为 5 组:第一组 85~100;第二组100~115;第三组 115~130;第四组 130~145;第五组 145~160,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:

(1)本次调查共随机抽取了该年级多少名学生?成绩为第五组的有多少名学生?
(2)针对考试成绩情况,现各组分别派出1名代表(分别用 A、B、C、D、E 表示5个小组中选出来的同学),命题教师从这5名同学中随机选出两名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名同学刚好来自第一、五组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=x+1的图象为直线l2,与x轴交于点C;两直线l1,l2相交于点B.
(1)求k、b的值;
(2)求点B的坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)6﹣4(x+2)=3(x﹣3)
(2)
 ﹣1
﹣1(3)
 =1
=1(4)

相关试题

