【题目】如图,MN为一电视塔,AB是坡角为30°的小山坡(电视塔的底部N与山坡的坡脚A在同一水平线上,被一个人工湖隔开),某数学兴趣小组准备测量这座电视塔的高度.在坡脚A处测得塔顶M的仰角为45°;沿着山坡向上行走40m到达C处,此时测得塔顶M的仰角为30°,请求出电视塔MN的高度.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)

参考答案:
【答案】95m
【解析】过点C作CE⊥AN于点E, CF⊥MN于点F.在△ACE中,求AE=20![]() m,在RT△MFC中,设MN=x m,则AN=xm.FC=
m,在RT△MFC中,设MN=x m,则AN=xm.FC=![]() xm,可得x+20
xm,可得x+20![]() =
=![]() ( x-20),解方程可得答案..
( x-20),解方程可得答案..
解:过点C作CE⊥AN于点E, CF⊥MN于点F.
在△ACE中,AC=40m,∠CAE=30°
∴CE=FN=20m,AE=20![]() m
m
设MN=x m,则AN=xm.FC=![]() xm,
xm,
在RT△MFC中
MF=MN-FN=MN-CE=x-20
FC=NE=NA+AE=x+20![]()
∵∠MCF=30°
∴FC=![]() MF,
MF,
即x+20![]() =
=![]() ( x-20)
( x-20)
解得:x=![]()
=60+20![]() ≈95m
≈95m
答:电视塔MN的高度约为95m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠MON内的一点,过点P作PA⊥OM于点A,PB⊥ON于点B,且OA=OB.
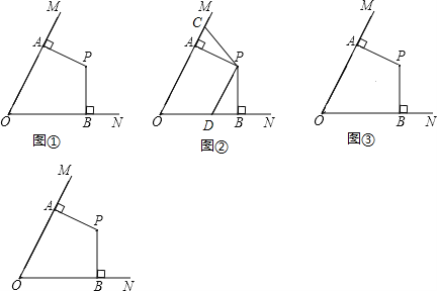
(1)求证:PA=PB;
(2)如图②,点C是射线AM上一点,点D是线段OB上一点,且∠CPD+∠MON=180°,若OC=8,OD=5.求线段OA的长.
(3)如图③,若∠MON=60°,将PB绕点P以每秒2°的速度顺时针旋转,12秒后,PA开始绕点P以每秒10°的速度顺时针旋转,PA旋转270°后停止,此时PB也随之停止旋转.旋转过程中,PA所在直线与OM所在直线的交点记为G,PB所在直线与ON所在直线的交点记为H.问PB旋转几秒时,PG=PH?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E为AB边上一点,DE=DC,点F为线段DE上一点,满足∠DFC=∠A,连结CE.
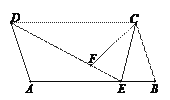
(1)求证:AD=FC;
(2)求证:CE是∠BCF的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,小明一家乘坐飞机前往某市旅游,计划第二天租出租车自驾游.
公司
租车收费方式
甲
每日固定租金80元,另外每小时收费15 元.
乙
无固定租金,直接以租车时间计费,每小时租费30元
(1)设租车时间为x小时
 , 租用甲公司的车所需费用为
, 租用甲公司的车所需费用为 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 元,分别求出
元,分别求出 与x之间的关系式:
与x之间的关系式:(2)请你帮助小明计算并选择哪个公司租车合算.
-
科目: 来源: 题型:
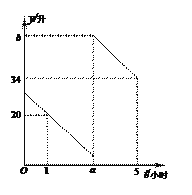
查看答案和解析>>【题目】张师傅驾驶某种型号轿车从甲地去乙地,该种型号轿车每百公里油耗为10升(每行驶100公里需消耗10升汽油).途中在加油站加了一次油,加油前,根据仪表盘显示,油箱中还剩4升汽油.假设加油前轿车以80公里/小时的速度匀速行驶,加油后轿车以90公里/小时的速度匀速行驶(不计加油时间),已知油箱中剩余油量y(升)与行驶时间t(小时)之间的函数关系如图所示.
(1) 加油前,该轿车每小时消耗汔油 升;加油后,该轿车每小时消耗汔油 升;
(2)求加油前油箱剩余油量y(升)与行驶时间t(小时)之间的函数表达式;
(3)求张师傅在加油站加了多少升汽油.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销甲、乙两种商品,现有如下信息:
信息1:甲商品的零售单价比乙商品的零售单价少1元;
信息2:按零售单价购买甲商品3件和乙商品2件,共付了12元.
请根据以上信息,解答下列问题:
(1)分别求甲、乙两种商品的零售单价;
(2)该商店平均每天卖出甲、乙两种商品各500件,经调查发现,两种商品零售单价每降0.1元,甲种商品每天可多销售30件,乙种商品每天可多销售20件,商店决定把两种商品的零售单价均下降m(0<m<1)元.在不考虑其他因素的条件下,当m为多少时,商店每天销售甲、乙两种商品的销售额之和为2500元?
相关试题

