【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.

(1)写出商场销售这种工具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
参考答案:
【答案】(1)w=-10x2+700x-10000;
(2)销售单价为35元时,每天销售利润最大,最大利润为2250元;
(3)方案A的最大利润更高,理由见解析.
【解析】试题分析:(1)根据利润=(销售单价-进价)×销售量,列出函数关系式即可;
(2)根据(1)式列出的函数关系式,运用配方法求最大值;
(3)分别求出方案A、B中x的取值范围,然后分别求出A、B方案的最大利润,然后进行比较.
试题解析:(1)w=(x-20)(250-10x+250)=-10x2+700x-10000.
(2)w=-10x2+700x-10000=-10(x-35)2+2250.
所以,当x=35时,w有最大值2250.
即销售单价为35元时,该文具每天的销售利润最大.
(3)方案A:由题可得20<x≤30,
因为a=-10<0,对称轴为x=35,
抛物线开口向下,在对称轴左侧,w随x的增大而增大,
所以,当x=30时,w取最大值为2000元.
方案B:由题意得![]() ,解得:
,解得: ![]() ,
,
在对称轴右侧,w随x的增大而减小,
所以,当x=45时,w取最大值为1250元.
因为2000元>1250元,
所以选择方案A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,点A的坐标是
中,点A的坐标是 ,点C的纵坐标是4,则B点的纵坐标是___________.
,点C的纵坐标是4,则B点的纵坐标是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0
(1)证明原方程有两个不相等的实数根;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示:AB=|x1﹣x2|)
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1、图2分别是
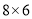 的网格,网格中每个小正方形的边长均为1,线段
的网格,网格中每个小正方形的边长均为1,线段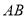 的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:
的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:(1)在图1中画一个以线段
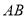 为一边且周长为
为一边且周长为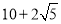 的平行四边形,所画图形的各顶点必须在小正方形的顶点上.
的平行四边形,所画图形的各顶点必须在小正方形的顶点上.(2)在图2中画一个以线段
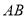 为一边的等腰钝角三角形,所画等腰三角形的各顶点必须在小正方形的顶点上,并直接写出该等腰三角形的周长是______.
为一边的等腰钝角三角形,所画等腰三角形的各顶点必须在小正方形的顶点上,并直接写出该等腰三角形的周长是______.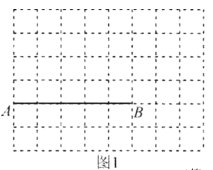
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布
次数
60≤x<80
80≤x<100
100≤x<120
频数
1
2
25
次数
120≤x<140
140≤x<160
160≤x<180
频数
15
5
2
(1)全班有多少学生?
(2)组距是多少?组数是多少
(3)跳绳次数x在100≤x<140范围的学生占全班学生的百分之几?
(4)画出适当的统计图表示上面的信息.
(5)你怎样评价这个班的跳绳成绩?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,海中有一个小岛
 ,它的周围14海里内有暗礁,在小岛正西方有一点
,它的周围14海里内有暗礁,在小岛正西方有一点 测得在北偏东60°方向上有一灯塔
测得在北偏东60°方向上有一灯塔 ,灯塔
,灯塔 在小岛
在小岛 北偏东15°方向上20海里处,渔船跟踪鱼群沿
北偏东15°方向上20海里处,渔船跟踪鱼群沿 方向航行,每小时航行
方向航行,每小时航行 海里.
海里.(1)如果渔船不改变航向继续航行,有没有触礁危险?请说明理由.
(2)求渔船从
 点处航行到灯塔
点处航行到灯塔 ,需要多少小时?
,需要多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,四边形ABCD是平行四边形,E,F是对角线AC上的两点,AE=CF.
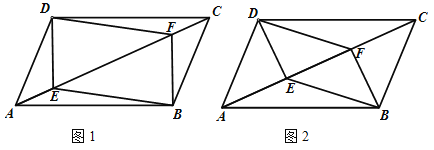
(1)求证:四边形DEBF是平行四边形;
(2)如果AE=EF=FC,请直接写出图中2所有面积等于四边形DEBF的面积的三角形.
相关试题

