搜索
【题目】已知:如图，已知∠1+∠2=180°，∠2=∠B，试说明∠DEC+∠C=180°，请完成下列填空：
证明:∵∠1+∠2=180°(已知)
∴_____∥_____(____________________)
∴______=∠EFC(____________________)
又∵2=∠B(已知)
∴∠2=______(等量代换)
∴___________(内错角相等,两直线平行)
∴∠DEC+∠C=180°(两直线平行,同旁内角互补)
参考答案：
【答案】AB、EF、同旁内角互补，两直线平行、∠B、两直线平行，同位角相等、∠EFC、DE//BC
【解析】
根据平行线的性质与判定求解即可.
证明:∵∠1+∠2=180°(已知)
∴_AB_∥__EF__(同旁内角互补，两直线平行)
∴_∠B __=∠EFC(_两直线平行，同位角相等__)
又∵∠2=∠B(已知)
∴∠2=__∠EFC _(等量代换)
∴__ DE//BC __(内错角相等,两直线平行)
∴∠DEC+∠C=180°(两直线平行,同旁内角互补)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，AM、BN分别与⊙O相切于点A、B，CD交AM、BN于点D、C，DO平分∠ADC.
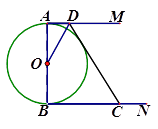
（1）求证：CD是⊙O的切线；
（2）设AD＝4，AB＝x (x > 0)，BC＝y (y > 0). 求y关于x的函数解析式. -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：已知点P（x0 ， y0）和直线y=kx+b，则点P到直线y=kx+b的距离，可用公式d=
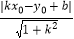计算．
例如：求点P（﹣1，2）到直线y=3x+7的距离．
解：因为直线y=3x+7，其中k=3，b=7．
所以点P（﹣1，2）到直线y=3x+7的距离为：d= =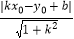 
= 
= 
．
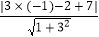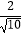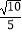根据以上材料，解答下列问题：
（1）求点P（1，﹣1）到直线y=x﹣1的距离；
（2）已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线y=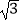
x+9的位置关系并说明理由；
（3）已知直线y=﹣2x+4与y=﹣2x﹣6平行，求这两条直线之间的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上的两点A、B所表示的数分别是a和b,O为数轴上的原点，如果有理数a,b满足
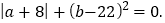
(1)求a和b的值；
(2)若点P是一个动点，以每秒5个单位长度的速度从点A出发，沿数轴向右运动，请问经过多长时间，点P恰巧到达线段AB的三等分点？
(3)若点C是线段AB的中点，点M以每秒3个单位长度的速度从点C开始向右运动，同时点P以每秒5个单位长度的速度从点A出发向右运动，点N以每秒4个单位长度的速度从点B开始向左运动，点P与点M之间的距离表示为PM，点P与点N之间的距离表示为PN，是否存在某一时刻使得PM+PN=12？若存在，请求出此时点P表示的数；若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的面积为1，分别倍长（延长一倍）AB，BC，CA得到△A1B1C1，再分别倍长A1B1，B1C1，C1A1得到△A2B2C2．…按此 规律，倍长n次后得到的△A2016B2016C2016的面积为__．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=
x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．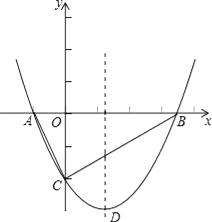
（1）求抛物线的解析式及顶点D的坐标；
（2）判断△ABC的形状，证明你的结论；
（3）点M是x轴上的一个动点，当△DCM的周长最小时，求点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】直线l：y=mx﹣m+1（m为常数，且m≠0）与坐标轴交于A、B两点，若△AOB（O是原点）的面积恰为2，则符合要求的直线l有（ ）
A.1条
B.2条
C.3条
D.4条
相关试题
