【题目】直线l:y=mx﹣m+1(m为常数,且m≠0)与坐标轴交于A、B两点,若△AOB(O是原点)的面积恰为2,则符合要求的直线l有( )
A.1条
B.2条
C.3条
D.4条
参考答案:
【答案】C
【解析】解:当x=0时,y=mx﹣m+1=1﹣m,
∴直线l与y轴的交点A的坐标为(0,1﹣m);
当y=mx﹣m+1=0时,x=1﹣ ![]() ,
,
∴直线l与x轴的交点B的坐标为(1﹣ ![]() ,0).
,0).
∵△AOB(O是原点)的面积恰为2,
∴ ![]() |1﹣m||1﹣
|1﹣m||1﹣ ![]() |=2.
|=2.
当m<0时,有m2+2m+1=0,
解得:m=﹣1;
当0<m≤1时,有m2﹣6m+1=0,
解得:m=3﹣2 ![]() 或m=3+2
或m=3+2 ![]() (舍去);
(舍去);
当m>1时,有m2﹣6m+1=0,
解得:m=3+2 ![]() 或m=3﹣2
或m=3﹣2 ![]() (舍去).
(舍去).
∴m的值有3个,即符合要求的直线有3个.
所以答案是:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列地方银行的标志中,既不是轴对称图形,也不是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )

A. 75°B. 60°C. 30°D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=
 EC,其中正确结论的序号是______.
EC,其中正确结论的序号是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=°.
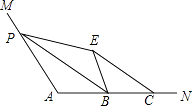
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列证明过程填空

如图,因为∠A=_____(已知),
所以AC∥ED( )
因为∠2=_____(已知),
所以AC∥ED( )
因为∠A+_____=180°(已知),
所以AB∥FD( )
因为AB∥_____(已知),
所以∠2+∠AED=180°( )
因为AC∥_____(已知),
所以∠C=∠3( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系中,点A(4,0),点B(m,
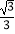 m),点C为线段OA上一点(点O为原点),则AB+BC的最小值为 .
m),点C为线段OA上一点(点O为原点),则AB+BC的最小值为 .
相关试题

