【题目】直线n与过原点的直线m交于点P,P点的坐标如图所示,直线n与y轴交于点A;若OA=OP;
(1)求A点的坐标;
(2)求直线m,n的函数表达式;
(3)求△AOP的面积.

参考答案:
【答案】(1)(0,﹣5);(2)y= ![]() x、y=2x﹣5;(3)
x、y=2x﹣5;(3)![]() .
.
【解析】
(1)利用勾股定理得出OP=OA=5,进而解答即可;
(2)把A、P点坐标代入直线n,把O、P点坐标代入直线m,再由待定系数法可求得直线的解析式;
(3)根据△ABC的面积公式解答即可.
(1)∵点P的坐标为(4,3),
∴OP=![]() =5,
=5,
∵OA=OP,
∴点A的坐标为(0,-5);
(2)设直线n的解析式为y1=kx+b,直线m的解析式为y2=ax,
把A、P点坐标代入直线n,可得:![]() ,
,
解得:![]() ,
,
把O、P点坐标代入直线m,可得:3=4a,
解得:a=![]() ,
,
所以直线m,n的函数表达式分别为:y=![]() x、y=2x-5;
x、y=2x-5;
(3)△AOP的面积=![]() ×5×3=
×5×3=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,∠BAC=90°,BC=6,过点C作CD⊥BC,CD=2,连接BD,过点C作CE⊥BD,垂足为E,连接AE,则AE长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为参加重庆市校园足球开幕式,某学校老师欲给演出学生租用男、女演出服装若干套以供开幕式伴舞用.已知5套男装和8套女装租用一天共需租金510元,6套男装和10套女装租用一天共需630元
(1)租用男装、女装一天的价格分别是多少?
(2)该节目原计划由6名男同学和17名女同学完成,后因节目需要,将其中3名女同学由伴舞角色转向歌手角色,歌手服装每套租用一天的价格比已选定女装价格贵20%,求在演出当天租用服装实际需支付租金多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图1,则有a2+b2=c2;若△ABC为锐角三角形时,小明猜想:a2+b2>c2 , 理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,AD2=b2﹣x2 , 在Rt△ADB中,AD2=c2﹣(a﹣x)2
∴a2+b2=c2+2ax
∵a>0,x>0
∴2ax>0
∴a2+b2>c2
∴当△ABC为锐角三角形时,a2+b2>c2
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系.
(2)温馨提示:在图3中,作BC边上的高.
(3)证明你猜想的结论是否正确. -
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
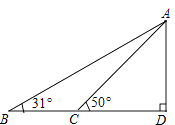
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题

(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?
(5)请你对“不及格”等级的同学提一个友善的建议(一句话即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.

(1)求证:BC为⊙O的切线.
(2)若sinA= ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.
相关试题

