[题目]如图.等腰直角△ABC中.∠BAC=90°.BC=6.过点C作CD⊥BC.CD=2.连接BD.过点C作CE⊥BD.垂足为E.连接AE.则AE长为．题目和参考答案 ——青夏教育精英家教网—

【题目】如图，等腰直角△ABC中，∠BAC=90°，BC=6，过点C作CD⊥BC，CD=2，连接BD，过点C作CE⊥BD，垂足为E，连接AE，则AE长为_____．

参考答案：

【答案】

【解析】根据旋转的性质得到△ABF≌△ACE，进而得出△AEF为等腰直角三角形，根据两角对应相等的两三角形相似的判定可得△BCD∽△BEC，然后根据对应边成比例可得，然后根据勾股定理即可求解.

把AE逆时针旋转90°，使AE=AF交BD于F，

根据旋转的性质可得△ABF≌△ACE，

即BF=CE，

∴△AEF是等腰直角三角形

∵CD⊥BC，CE⊥BD

∴∠BCD=∠CEB=90°

∵∠DBC=∠CBD，

∴△BCD∽△BEC

∴

∵BC=6，CD=2

∴BD==

即CE=

∴DE=

即BE=

∴EF=——=

∴AE=AF=

故答案为：.

相关试题

科目： 来源： 题型：

【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；
（2）设∠BAC= ，∠DCE= ．
① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究与之间的数量关系，并证明你的结论；
② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时与之间的数量关系（不需证明）．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．
（1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，矩形ABCD中，AB=8，BC=6．点E在边AB上，点F在边CD上，点G、H在对角线AC上．若四边形EGFH是菱形，则AE的长是（　　）
A. 2 B. 3 C. D.
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在等边三角形ABC中，AB=5，在AB边上有一点P，过点P作PM⊥BC，垂足为M，过点M作MN⊥AC，垂足为N，过点N作NQ⊥AB，垂足为Q．当PQ=1时，BP=_____．
查看答案和解析>>
科目： 来源： 题型：

【题目】已知抛物线的不等式为y=﹣x2+6x+c．
（1）若抛物线与x轴有交点，求c的取值范围；
（2）设抛物线与x轴两个交点的横坐标分别为x1 ， x2 ．若x12+x22=26，求c的值．
（3）若P，Q是抛物线上位于第一象限的不同两点，PA，QB都垂直于x轴，垂足分别为A，B，且△OPA与△OQB全等．求证：c＞﹣ ．
查看答案和解析>>
科目： 来源： 题型：

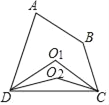
【题目】如图，在四边形ABCD中，∠A+∠B=200°，作∠ADC、∠BCD的平分线交于点O1称为第1次操作，作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作，作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作，…，则第5次操作后∠CO5D的度数是_____．
查看答案和解析>>