【题目】如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°. 
(1)求证:BC为⊙O的切线.
(2)若sinA= ![]() ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.
参考答案:
【答案】
(1)证明:∵∠A与∠E所对的弧都是 ![]() ,
,
∴∠A=∠E,
又∵∠E+∠C=90°,
∴∠A+∠C=90°,
在△ABC中,∠ABC=180°﹣90°=90°,
∵AB为直径,
∴BC为⊙O的切线
(2)解:∵sinA= ![]() ,BC=6,
,BC=6,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得AC=10,
由勾股定理得,AB= ![]() =
= ![]() =8,
=8,
∵AB为直径,
∴⊙O的半径是 ![]() ×8=4
×8=4
【解析】(1)根据在同圆或等圆中,同弧所对的圆周角相等可得∠A=∠E,再根据三角形的内角和等于180°求出∠ABC=90°,然后根据切线的定义证明即可;(2)根据∠A的正弦求出AC,利用勾股定理列式计算求出AB,然后求解即可.本题考查了切线的判定,锐角三角函数,解直角三角形,勾股定理,在同圆或等圆中,同弧所对的圆周角相等的性质,熟记切线的概念并求出直角是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线n与过原点的直线m交于点P,P点的坐标如图所示,直线n与y轴交于点A;若OA=OP;
(1)求A点的坐标;
(2)求直线m,n的函数表达式;
(3)求△AOP的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
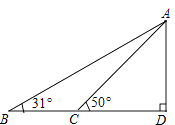
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题

(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?
(5)请你对“不及格”等级的同学提一个友善的建议(一句话即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
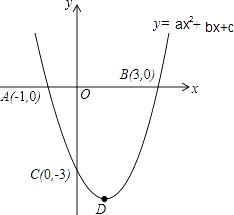
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,我们在“格点”直角坐标系上可以看到,要求AB或CD的长度,可以转化为求Rt△ABC或Rt△DEF的斜边长.
例如:从坐标系中发现:D(﹣7,3),E(4,﹣3),所以DF=|5﹣(﹣3)|=8,EF=|4﹣(﹣7)|=11,所以由勾股定理可得:DE=
 .
.(1)在图①中请用上面的方法求线段AB的长:AB= ;
(2)在图②中:设A(x1,y1),B(x2,y2),试用x1,x2,y1,y2表示:AC= ,BC= ,AB= ;
(3)试用(2)中得出的结论解决如下题目:已知:A(2,1),B(4,3);
①直线AB与x轴交于点D,求线段BD的长;
②C为坐标轴上的点,且使得△ABC是以AB为边的等腰三角形,请求出C点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
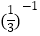 +|1﹣
+|1﹣ 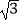 |﹣2sin60°+(π﹣2016)0﹣
|﹣2sin60°+(π﹣2016)0﹣  .
.
相关试题

