【题目】已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数 ![]() 的图象经过点C,且与AB交于点E,若OD=2,则△OCE的面积为 .
的图象经过点C,且与AB交于点E,若OD=2,则△OCE的面积为 . 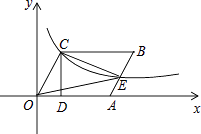
参考答案:
【答案】4 ![]()
【解析】解:过点E作EF⊥x轴于点F,如图所示. 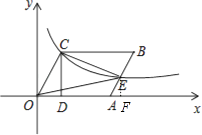
∵OD=2,
∴点C的横坐标为2,
∵点C在反比例函数y= ![]() 的图象上,
的图象上,
∴点C的坐标为(2,4),
∴直线OC的解析式为y=2x,OC= ![]() =2
=2 ![]() .
.
∵四边形OABC是菱形,
∴OA=OC=2 ![]() ,
,
∴直线AB的解析式为y=2(x﹣2 ![]() )=2x﹣4
)=2x﹣4 ![]() .
.
联立直线AB的解析式和反比例函数解析式成方程组: 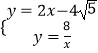 ,
,
解得: ![]() (舍去),或
(舍去),或 ![]() ,
,
∴点E的坐标为(3+ ![]() ,6﹣2
,6﹣2 ![]() ).
).
S△OCE=S△OCD+S梯形CDFE﹣S△OEF=S梯形CDFE= ![]() (CD+EF)DF=
(CD+EF)DF= ![]() (yC+yE)(xE﹣xC)=
(yC+yE)(xE﹣xC)= ![]() ×(4+6﹣2
×(4+6﹣2 ![]() )×(3+
)×(3+ ![]() ﹣2)=4
﹣2)=4 ![]() .
.
故答案为:4 ![]() .
.
由OD=2结合反比例函数的解析式可得出点C的坐标,由此即可得出直线OC的解析式和线段OC的长度,根据菱形的性质结合平移的性质即可得出直线AB的解析式,联立直线AB的解析式与反比例函数的解析式成方程组,解方程组即可得出点E的坐标,再通过分割图形求面积法找出S△OCE=S梯形CDFE , 利用梯形的面积公式即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠MON=45°,OA1=1,作正方形A1B1C1A2 , 面积记作S1;再作第二个正方形A2B2C2A3 , 面积记作S2;继续作第三个正方形A3B3C3A4 , 面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是( )

A.256
B.900
C.1024
D.4096 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.若⊙O的半径为5,cos∠BCD=
 ,那么线段AD= .
,那么线段AD= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个白色六边形相邻.若一段边框上有45个黑色六边形,则这段边框共有白色六边形( )

A. 182个 B. 180个 C. 272个 D. 270个
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题
 ,小虎马上举手,要求到黑板上去做,他是这样做的:
,小虎马上举手,要求到黑板上去做,他是这样做的:5(3x-1)=2(4x+2)-1①,
15x-5=8x+4-1②,
15x-8x=4-1+5③
7x④,
x=
 ⑤
⑤老师说:小虎解一元一次方程的一般步骤都知道,但没有掌握好,因此解题出现了错误,请指出他的错步及错误原因: ,方程的正确的解是x= .
然后,你自己细心的解下面的方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC.
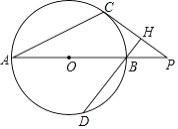
(1)求证:PC是⊙O的切线;
(2)若sin∠P=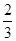 ,求
,求 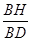 的值.
的值. -
科目: 来源: 题型:
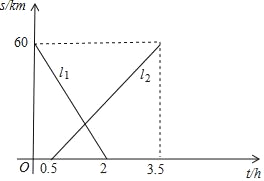
查看答案和解析>>【题目】A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中
 表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:(1)表示乙离A地的距离与时间关系的图象是 (填
 或
或 );
);(2)甲的速度是 km/h,乙的速度是 km/h;
(3)甲出发多少小时两人恰好相距5km?
相关试题

