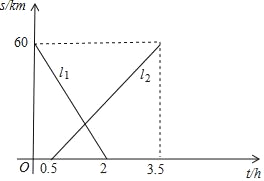
【题目】A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填![]() 或
或![]() );
);
(2)甲的速度是 km/h,乙的速度是 km/h;
(3)甲出发多少小时两人恰好相距5km?
参考答案:
【答案】(1)l2;(2)30,20;(3)1.3或1.5.
【解析】
(1)观察图象即可知道乙的函数图象为l2;
(2)根据速度=![]() ,利用图中信息即可解决问题;
,利用图中信息即可解决问题;
(3)分相遇前或相遇后两种情形分别列出方程即可解决问题;
(1)由题意可知,乙的函数图象是l2;
(2)甲的速度是![]() =30km/h,乙的速度是
=30km/h,乙的速度是![]() =20km/h.
=20km/h.
(2)设甲出发x小时两人恰好相距5km.由题意得:
30x+20(x﹣0.5)+5=60或30x+20(x﹣0.5)﹣5=60
解得:x=1.3或1.5.
答:甲出发1.3小时或1.5小时两人恰好相距5km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数
 的图象经过点C,且与AB交于点E,若OD=2,则△OCE的面积为 .
的图象经过点C,且与AB交于点E,若OD=2,则△OCE的面积为 . 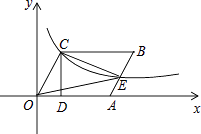
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题
 ,小虎马上举手,要求到黑板上去做,他是这样做的:
,小虎马上举手,要求到黑板上去做,他是这样做的:5(3x-1)=2(4x+2)-1①,
15x-5=8x+4-1②,
15x-8x=4-1+5③
7x④,
x=
 ⑤
⑤老师说:小虎解一元一次方程的一般步骤都知道,但没有掌握好,因此解题出现了错误,请指出他的错步及错误原因: ,方程的正确的解是x= .
然后,你自己细心的解下面的方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC.
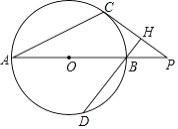
(1)求证:PC是⊙O的切线;
(2)若sin∠P=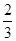 ,求
,求 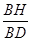 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表. 对雾霾了解程度的统计表:
对雾霾的了解程度
百分比
A.非常了解
5%
B.比较了解
m
C.基本了解
45%
D.不了解
n
请结合统计图表,回答下列问题.
对雾霾天气了解程度的条形统计图
对雾霾天气了解程度的扇形统计图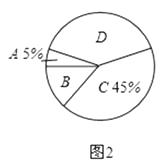
(1)本次参与调查的学生共有人,m= , n=;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
相关试题

