搜索
【题目】如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（﹣3，4），B（﹣5，2），C（﹣2，1）．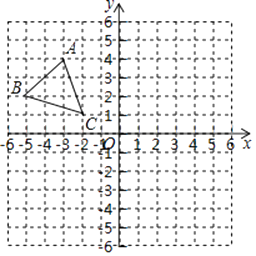
（1）画出△ABC关于y轴对称图形△A1B1C1；
（2）画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2；
（3）求（2）中线段OA扫过的图形面积．
参考答案：
【答案】
（1）
解：如图，△A1B1C1即为所求；
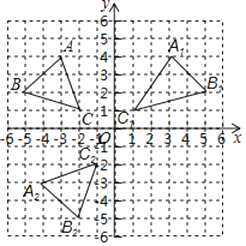
（2）
解：如图，△A2B2C2即为所求；
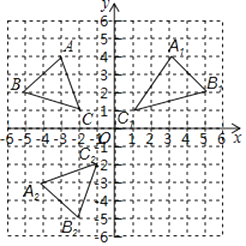
（3）
解：∵OA= 
=5，
∴线段OA扫过的图形面积= 
= 
π．
【解析】（1）分别作出各点关于y轴的对称点，再顺次连接即可；（2）根据图形旋转的性质画出旋转后的图形△A2B2C2即可；（3）利用扇形的面积公式即可得出结论．
【考点精析】本题主要考查了扇形面积计算公式和作轴对称图形的相关知识点，需要掌握在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）；画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，点A的坐标为（4，﹣3），且OA＝5，在x轴上确定一点P，使△AOP为等腰三角形．
（1）写出一个符合题意的点P的坐标 ；
（2）请在图中画出所有符合条件的△AOP．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知O是坐标原点，点A的坐标是（5，0），点B是y轴正半轴上一动点，以OB、OA为边作矩形OBCA，点E、H分别在边BC和边OA上，将△BOE沿着OE对折，使点B落在OC上的F点处，将△ACH沿着CH对折，使点A落在OC上的G点处．
（1）如图1，求证：四边形OECH是平行四边形；
（2）如图2，当点B运动到使得点F、G重合时，求点B的坐标，并判断四边形OECH是什么四边形？说明理由；
（3）当点B运动到使得点F，G将对角线OC三等分时，如图3，如图4，分别求点B的坐标．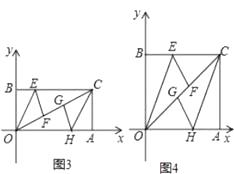
-
科目： 来源： 题型：
查看答案和解析>>【题目】电影《中国机长》是根据2018年5月14日川航3U8633航班的真实事件改编的，当时飞机挡风玻璃在高空爆裂，机组临危不乱、果断应对，顺利返航．下表给出了飞机距离地面高度
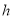与所在位置温度
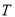的部分统计数据，根据下表，请回答以下问题：距离地面高度
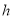（千米）0
1
2
3
4
5
所在位置的温度
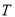（℃）20
14
_____
2
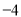
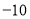
（1）上表反映的两个变量中，________是自变量，________是因变量；
（2）用关系式表示上表两个变量之间的关系：________；
（3）如图是当日飞机下降过程中距地面高度
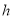与玻璃爆裂后立即返回地面所用时间
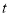的关系图．根据图象回答以下问题：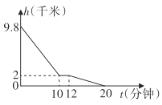
①返回途中飞机在2千米高空水平盘旋了几分钟？
②飞机盘旋时所在高空的温度是多少？
-
科目： 来源： 题型：
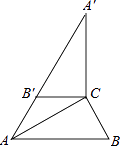
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为（ ）
A.6
B.4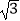
C.3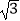
D.3 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB=16，O为AB中点，点C在线段OB上（不与点O，B重合），将OC绕点O逆时针旋转270°后得到扇形COD，AP，BQ分别切优弧
于点P，Q，且点P，Q在AB异侧，连接OP． 
（1）求证：AP=BQ；
（2）当BQ=4
时，求 
的长（结果保留π）；
（3）若△APO的外心在扇形COD的内部，求OC的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】看图填空，并在括号内说明理由：
∵BD平分∠ABC（已知）
∴__________=__________（__________）
又∠1=∠D（已知）
∴__________=__________（__________）
∴__________∥__________（__________）
∴∠ABC+__________=180°（__________）
又∠ABC=55°（已知）
∴∠BCD=__________．
相关试题
