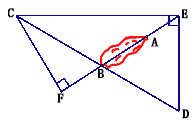
【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=![]() .
.
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.
参考答案:
【答案】(1) 16.7(海里).(2) ![]() .
.
【解析】
试题分析:(1)在Rt△CED中,利用三角函数求出CE,CD的长,根据中点的定义求得BE的长,AB=BE-AE即可求解;
(2)设BF=x海里.在Rt△CFB中,利用勾股定理求得CF2=CB2-BF2=252-x2=625-x2.在Rt△CFE中,列出关于x的方程,求得x的值,从而求得sin∠BCF的值.
(1)在Rt△CED中,∠CED=90°,DE=30海里,
∴cos∠D=![]() ,
,
∴CE=40(海里),CD=50(海里).
∵B点是CD的中点,
∴BE=![]() CD=25(海里)
CD=25(海里)
∴AB=BE-AE=25-8.3=16.7(海里).
答:小岛两端A、B的距离为16.7海里.
(2)设BF=x海里.
在Rt△CFB中,∠CFB=90°,
∴CF2=CB2-BF2=252-x2=625-x2.
在Rt△CFE中,∠CFE=90°,
∴CF2+EF2=CE2,即625-x2+(25+x)2=1600.
解得x=7.
∴sin∠BCF=![]() .
.
考点: 解直角三角形的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y﹣2与x成正比例,当x=2时,y=6.
(1)求y与x之间的函数解析式.
(2)在所给直角坐标系中画出函数图象.
(3)由函数图象直接写出当﹣2≤y≤2时,自变量x的取值范围.

-
科目: 来源: 题型:
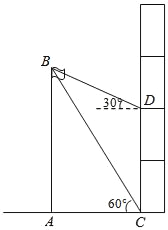
查看答案和解析>>【题目】如图,江阴实验中学初三研究性学习小组要测量学校旗杆AB的高度,首先在初三楼一楼C 处测得旗杆顶部的仰角为60°,然后在初三楼三楼D处测得旗杆顶部的仰角为30°,已知旗杆底部与教学楼一楼在同一水平线上,若CD=8米,求旗杆AB的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是八(1)班学生身高的统计表和扇形统计图,请回答以下问题:
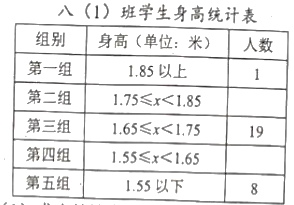
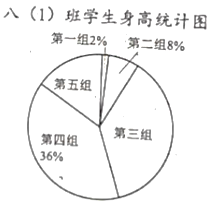
(1)求出统计表和统计图缺的数据.
(2)八(1)班学生身高这组数据的中位数落在第几组?
(3)如果现在八(1)班学生的平均身高是1.63m,已确定新学期班级转来两名新同学,新同学的身高分别是1.54m和1.77m,那么这组新数据的中位数落在第几组?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C是直线AB上一点,AC=6cm,BC=4cm,点M、N分别是AC、BC的中点;
(1)如图,点C在线段AB上,求线段MN的长;
(2)若点C在线段AB的延长线上,其他条件不变,则线段MN的长为_______cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用同样大小的黑色棋子按如图所示的规律摆放:

(1)分别写出第6、7两个图形各有多少颗黑色棋子?
(2)写出第n个图形黑色棋子的颗数?
(3)是否存在某个图形有1020颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.
相关试题

