【题目】如图,在四边形![]() 中,
中,![]() 、
、![]() 为对角线,点
为对角线,点![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 边的中点,下列说法:
边的中点,下列说法:
①当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
②当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
③当![]() 且
且![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
参考答案:
【答案】C
【解析】
连接EM、MF、FN、NE,连接EF、MN,交于点O,利用三角形中位线定理可证到四边形ENFM是平行四边形;然后根据条件判定四边形ENFM的形状,就可知道M、E、N、F四点是否共圆.
解:连接EM、MF、FN、NE,连接EF、MN,交于点O,如图所示.
∵点M、E、N、F分别为AD、AB、BC、CD边的中点,
∴EM∥BD∥NF,EN∥AC∥MF,EM=NF=![]() BD,EN=MF=
BD,EN=MF=![]() AC.
AC.
∴四边形ENFM是平行四边形.
①当AC=BD时,
则有EM=EN,
所以平行四边形ENFM是菱形.
而菱形的四个顶点不一定共圆,
故①不一定正确.
②当AC⊥BD时,
由EM∥BD,EN∥AC可得:EM⊥EN,即∠MEN=90°.
所以平行四边形ENFM是矩形.
则有OE=ON=OF=OM.
所以M、E、N、F四点共圆,
故②正确.
③当AC=BD且AC⊥BD时,
同理可得:四边形ENFM是正方形.
则有OE=ON=OF=OM
所以M、E、N、F四点共圆,
故③正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的对角线相交于点
的对角线相交于点 ,
, ,
, .
.
 求证:四边形
求证:四边形 是菱形;
是菱形; 若
若 ,菱形
,菱形 的面积为
的面积为 ,求
,求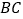 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(a,0),B(0,b),且a、b满足
 .
.(1)填空:a= ,b= ;
(2)如图1,将ΔAOB沿x轴翻折得ΔAOC,D为线段AB上一动点,OE⊥OD交AC于点E,求S四边形ODAE。
(3)如图2,D为AB上一点,过点B作BF⊥OD于点G,交x轴于点F,点H为x轴正半轴上一点,∠BFO=∠DHO,求证:AF=OH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是矩形
是矩形 的对角线的交点,
的对角线的交点, 、
、 、
、 、
、 分别是
分别是 、
、 、
、 、
、 上的点,且
上的点,且 .
.
 求证:四边形
求证:四边形 是矩形;
是矩形; 若
若 、
、 、
、 、
、 分别是
分别是 、
、 、
、 、
、 的中点,且
的中点,且 ,
,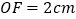 ,求矩形
,求矩形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点EF是中线AD上的两点,则图中全等三角形有几对( )
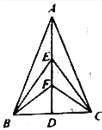
A.4对B.5对C.6对D.7对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
, 相交于点
相交于点 ,
, 平分
平分 交
交 于点
于点 ,若
,若 ,则
,则 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点
,点 、
、 分别在
分别在 、
、 上,连接
上,连接 ,
, 、
、 的平分线交于点
的平分线交于点 ,
, 、
、 的平分线交于点
的平分线交于点 .
.
 求证:四边形
求证:四边形 是矩形.
是矩形. 小明在完成
小明在完成 的证明后继续进行了探索,过点
的证明后继续进行了探索,过点 作
作 ,分别交
,分别交 、
、 于点
于点 、
、 ,过点
,过点 作
作 ,分别交
,分别交 、
、 于点
于点 、
、 ,得到四边形
,得到四边形 .此时,他猜想四边形
.此时,他猜想四边形 是菱形.请在下列框图中补全他的证明思路.
是菱形.请在下列框图中补全他的证明思路.小明的证明思路:由
 ,
, ,
, 易证,四边形
易证,四边形 是平行四边形.要证□
是平行四边形.要证□ 是菱形,只要证
是菱形,只要证 .由已知条件________,
.由已知条件________, ,可证
,可证 ,故只要证
,故只要证 ,即证
,即证 ,易证________,________,故只要证
,易证________,________,故只要证 ,易证
,易证 ,
, ,________,故得
,________,故得 ,即可得证.
,即可得证.
相关试题

