【题目】已知A(a,0),B(0,b),且a、b满足![]() .
.
(1)填空:a= ,b= ;
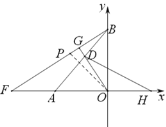
(2)如图1,将ΔAOB沿x轴翻折得ΔAOC,D为线段AB上一动点,OE⊥OD交AC于点E,求S四边形ODAE。
(3)如图2,D为AB上一点,过点B作BF⊥OD于点G,交x轴于点F,点H为x轴正半轴上一点,∠BFO=∠DHO,求证:AF=OH.

参考答案:
【答案】(1)a=-3,b=3;(2)4.5;(3)见解析.
【解析】
(1)根据二次根式的性质及绝对值的非负性可得:a+3=0,a+b=0,求出a、b即可;
(2)根据条件先证明△BOD≌△AOE,然后将四边形ODAE的面积转化为△AOB的面积进行计算即可;
(3)过点O作OP平分∠AOB交BF于P,先证明△BOP≌△OAD,推出OP=AD,再证明△PFO≌△DHA,利用全等的性质即可得出结论.
解:(1)∵a、b满足![]() ,
,
∴a+3=0,a+b=0,
∴a=-3,b=3;
(2)∵由(1)知:A(-3,0),B(0,3)
∴OA=OB=3
∵△AOB沿x轴翻折得△AOC
∴OA=OB=OC,∠AOB=∠AOC=90°
∴∠ABO=∠BAO=∠CAO=45°
又∵OE⊥OD,且∠BOD+∠AOD =∠AOB=90°
∴∠AOE+∠AOD=∠BOD+∠AOD=90°
∴∠AOE=∠BOD
∵∠DBO=∠EAO,OB=OA,∠BOD=∠AOE
∴△BOD≌△AOE(ASA)
∴S△AOE=S△BOD
∴S四边形ODAE=S△AOE + S△AOD = S△BOD + S△AOD =S△AOB=![]() ;
;
(3)过点O作OP平分∠AOB交BF于P,
∵OP平分∠AOB且OA=OB
∴∠AOP=∠BOP=45°
∴∠AOP=∠BOP=∠OAD
∵BG⊥OD
∴∠OBP+∠BOG=90°
又∵∠AOD+∠BOG=90°
∴∠OBP=∠AOD
∵OB=OA
∴△BOP≌△OAD(ASA)
∴OP=AD
又∵∠PFO=∠DHO,∠FOP=∠HAD=45°
∴△PFO≌△DHA(AAS)
∴OF=AH
∴OF-OA=AH-OA,即AF=OH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,点D在BC上,△ADE是等腰三角形,AD =AE ,∠DAE =100°,当DE⊥AC时,求∠BAD和∠EDC的度数.
-
科目: 来源: 题型:
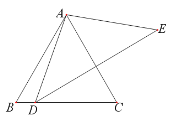
查看答案和解析>>【题目】如图,△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,E在线段AC上,连接AD, BE的延长线交AD于F.
(1)猜想线段BE、AD的数量关系和位置关系:_______________(不必证明);
(2)当点E为△ABC内部一点时,使点D和点E分别在AC的两侧,其它条件不变.
①请你在图2中补全图形;
②(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的对角线相交于点
的对角线相交于点 ,
, ,
, .
.
 求证:四边形
求证:四边形 是菱形;
是菱形; 若
若 ,菱形
,菱形 的面积为
的面积为 ,求
,求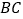 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是矩形
是矩形 的对角线的交点,
的对角线的交点, 、
、 、
、 、
、 分别是
分别是 、
、 、
、 、
、 上的点,且
上的点,且 .
.
 求证:四边形
求证:四边形 是矩形;
是矩形; 若
若 、
、 、
、 、
、 分别是
分别是 、
、 、
、 、
、 的中点,且
的中点,且 ,
,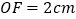 ,求矩形
,求矩形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中, 、
、 为对角线,点
为对角线,点 、
、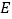 、
、 、
、 分别为
分别为 、
、 、
、 、
、 边的中点,下列说法:
边的中点,下列说法:①当
 时,
时, 、
、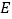 、
、 、
、 四点共圆.
四点共圆.②当
 时,
时, 、
、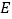 、
、 、
、 四点共圆.
四点共圆.③当
 且
且 时,
时, 、
、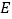 、
、 、
、 四点共圆.
四点共圆.其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点EF是中线AD上的两点,则图中全等三角形有几对( )
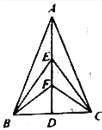
A.4对B.5对C.6对D.7对
相关试题

