【题目】已知一个等腰三角形两边长之比为1:4,周长为18,则这个等腰三角形底边长为( )
A.2B.6C.8D.2或8
参考答案:
【答案】A
【解析】
题中只给出了两边之比,没有明确说明哪个是底哪个是腰,所以应该分两种情况进行分析,再结合三角形三边的关系将不合题意的解舍去.
因为两边长之比为1:4,所以设较短一边为x,则另一边为4x;
(1)假设x为底边,4x为腰;则8x+x=18,x=2,即底边为2;
(2)假设x为腰,4x为底边,则2x+4x=18,x=3,4x=12;
∵3+3<12,∴该假设不成立.
所以等腰三角形的底边为2.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2,若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=﹣x2先向下平移2个单位,再向右平移3个单位后所得抛物线的解析式为 .
-
科目: 来源: 题型:
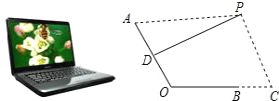
查看答案和解析>>【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据:
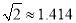 ,
, 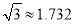 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,结果正确的是( )
A.(a3)2=a6
B.(ab)3=a3b
C.aa3=a3
D.a8÷a4=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+3的图象与直线y=2x平行,那么此一次函数的表达式为______.
-
科目: 来源: 题型:
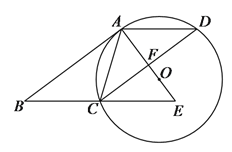
查看答案和解析>>【题目】如图,在□ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交于E.
(1)求证:AB是⊙O的切线;
(2)若AB=8,AD=5,求OE的长.
相关试题

