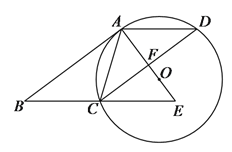
【题目】如图,在□ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交于E.
(1)求证:AB是⊙O的切线;
(2)若AB=8,AD=5,求OE的长.
参考答案:
【答案】(1)证明参见解析;(2)![]() .
.
【解析】试题分析:(1)由已知得出弧AC=弧AD,由垂径定理得出OA⊥CD,由平行四边形的性质得出AB∥CD,AD∥BC,AD=BC,因此OA⊥AB,即可得出结论;(2)连接OD,由垂径定理得出CF=DF=4,由平行线得出△ADF∽△ECF,得出对应边成比例,证出AD=CE,AF=EF,得出BC=CE,BE=10,由勾股定理求出AE,得出AF=EF=3,设OE=x,则OF=3﹣x,⊙O的半径为6﹣x,由勾股定理得出方程,解方程即可.
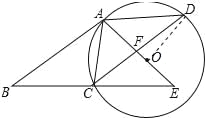
试题解析:(1)∵AC=AD,∴弧AC=弧AD,∴OA⊥CD,∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,AD=BC,∴OA⊥AB,∴AB是⊙O的切线;(2)连接OD,如图所示:∵OA⊥CD,∴CF=DF=4,∵AD∥BC,∴△ADF∽△ECF,∴![]() =1,∴AD=CE,AF=EF,∴BC=CE,∴BE=2BC=2AD=10,∴AE=
=1,∴AD=CE,AF=EF,∴BC=CE,∴BE=2BC=2AD=10,∴AE=![]() =6,∴AF=EF=3,设OE=x,则OF=3﹣x,⊙O的半径为6﹣x,由勾股定理得:OF2+DF2=OD2,即(6﹣x)2=(3﹣x)2+42,解得:x=
=6,∴AF=EF=3,设OE=x,则OF=3﹣x,⊙O的半径为6﹣x,由勾股定理得:OF2+DF2=OD2,即(6﹣x)2=(3﹣x)2+42,解得:x=![]() ,即OE=
,即OE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形两边长之比为1:4,周长为18,则这个等腰三角形底边长为( )
A.2B.6C.8D.2或8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,结果正确的是( )
A.(a3)2=a6
B.(ab)3=a3b
C.aa3=a3
D.a8÷a4=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+3的图象与直线y=2x平行,那么此一次函数的表达式为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各多项式中,不能用平方差公式分解的是( )
A.a2b2﹣1
B.1﹣0.25a2
C.﹣a2﹣b2
D.﹣x2+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,4),B(﹣4,a)在双曲线y=
 图象上,直线AB分别交x轴,y轴于C、D,过点A作AE⊥x轴,垂足为E,过点B作BF⊥y轴,垂足为F,连接AF、BE交于点G.
图象上,直线AB分别交x轴,y轴于C、D,过点A作AE⊥x轴,垂足为E,过点B作BF⊥y轴,垂足为F,连接AF、BE交于点G.(1)求k的值及直线AB的解析式;
(2)判断四边形ADFE的形状,并写出证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校“我的中国梦”演讲比赛中,有7名学生参加决赛,他们决赛的最终成绩各不相同,其中一名学生想要知道自己能否进入前3名,他不仅要了解自己的成绩,还要了解这7名学生成绩的( )
A.众数
B.方差
C.平均数
D.中位数
相关试题

